
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, Xét tam giác DEB và tam giác DFC ta có
BD = DC (gt)
^B = ^C (gt)
Vậy tam giác DEB = tam giác DFC (ch-gn)
=> DE = DF ( 2 cạnh tương ứng )
b, Xét tam giác AED và tam giác AFD có
AD _ chung
DE = DF (cmt)
Vậy tam giác AED = tam giác AFD (ch-cgv)
=> ^EAD = ^FAD ( góc tương ứng )
b, Xét tam giác ABC có
^EAD = ^FAD (cmt) hay AD là phân giác ^A
Bạn ới, sao câu b nó sao sao ấy, chỗ "Xét tam giác ABC" ấy, mik thấy hơi hơi kì phải hong bạn hay bài làm đúm rùi?🤔🤔🤧🤧

=)) Mik chịu á, bạn cứ làm mấy chỗ khác trước và chừa chứng minh cho mik cx đc ạ

a: Xét ΔAOC và ΔBOC có
OA=OB
\(\widehat{AOC}=\widehat{BOC}\)
OC chung
DO đó: ΔAOC=ΔBOC
b: Xét tứ giác OAEB có
C là trung điểm của OE
C là trung điểm của AB
Do đó: OAEB là hình bình hành
Suy ra: AE//OB

1: \(BC=\sqrt{AB^2+AC^2}=5\left(cm\right)\)
2: \(MN=\sqrt{15^2-12^2}=9\left(cm\right)\)
3: \(AC=3cm\)
4: \(\widehat{B}=\widehat{C}=\dfrac{180^0-30^0}{2}=75^0\)

a: Xét ΔDBE có DB=DE
nên ΔDBE cân tại D
hay \(\widehat{DBE}=\widehat{DEB}\)
b: Ta có: \(\widehat{MBE}+\widehat{DEB}=90^0\)
\(\widehat{EBN}+\widehat{DBE}=90^0\)
mà \(\widehat{DBE}=\widehat{DEB}\)
nên \(\widehat{MBE}=\widehat{NBE}\)
hay BE là tia phân giác của góc MBN
c: Xét ΔMBE vuông tại M và ΔNBE vuông tại N có
BE chung
\(\widehat{MBE}=\widehat{NBE}\)
Do đó: ΔMBE=ΔNBE
Suy ra: EM=EN
d: Ta có: ΔMBE=ΔNBE
nên BM=BN
hay B nằm trên đường trung trực của MN(1)
Ta có:EM=EN
nên E nằm trên đường trung trực của MN(2)
Từ (1) và (2) suy ra BE là đường trung trực của MN

10: Chọn B
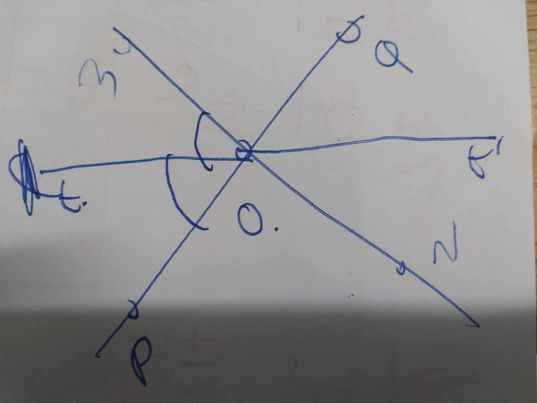
Ot là phân giác của \(\widehat{MOP}\)
=>\(\widehat{MOP}=2\cdot\widehat{tOP}\)
\(\widehat{MOP}=\widehat{NOQ}\)
=>\(\widehat{NOQ}=2\cdot\widehat{tOP}\)
mà \(\widehat{tOP}=\widehat{t'OQ}\)(hai góc đối đỉnh)
nên \(\widehat{NOQ}=2\cdot\widehat{t'OQ}\)
=>Ot' là phân giác của góc NOQ
11:
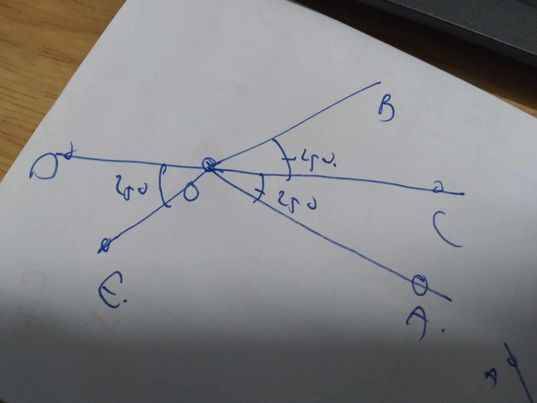
OC là phân giác của góc AOB
=>\(\widehat{AOC}=\widehat{BOC}=\dfrac{50^0}{2}=25^0\)
\(\widehat{DOE}=\widehat{BOC}\left(=25^0\right)\)
=>\(\widehat{DOE}+\widehat{DOB}=180^0\)
=>OB và OE là hai tia đối nhau
=>Hai góc đối đỉnh là \(\widehat{BOC};\widehat{DOE}\)
=>Chọn D
12:
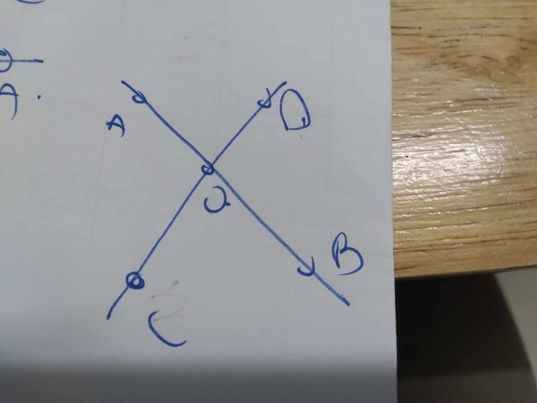
\(\widehat{AOC}+\widehat{AOD}=180^0\)
\(\widehat{AOC}-\widehat{AOD}=50^0\)
Do đó: \(\widehat{AOC}=\dfrac{180^0+50^0}{2}=115^0;\widehat{AOD}=115^0-50^0=65^0\)
=>\(\widehat{BOC}=\widehat{AOD}=65^0\)
=>Chọn B

b: Xét ΔDEM và ΔDFM có
DE=DF
\(\widehat{EDM}=\widehat{FDM}\)
DM chung
Do đó: ΔDEM=ΔDFM
c: Xét ΔDEF có
DM là đường trung tuyến
G là trọng tâm
Do đó: D,G,M thẳng hàng

Bài 4:
a: \(BC=\sqrt{8^2+6^2}=10\left(cm\right)\)
b: Xét ΔEDB có
EA là đường cao
EA là đường trung tuyến
Do đó:ΔEDB cân tại E
Xét ΔCDB có
CA là đường cao
CA là đường trung tuyến
Do đó: ΔCDB cân tại C
Xét ΔCDE và ΔCBE có
CD=CB
ED=EB
CE chung
Do đó: ΔCDE=ΔCBE
c: Xét ΔCDB có
CA là đường trung tuyến
CE=2/3CA
Do đó: E là trọng tâm của ΔCDB
Suy ra: DE đi qua trung điểm của BC

 Các bạn giải cả 3 bài này giúp mình với, mình đang gấp nhớ vẽ hình lun ạ !!! Cảm ơn
Các bạn giải cả 3 bài này giúp mình với, mình đang gấp nhớ vẽ hình lun ạ !!! Cảm ơn


 vẽ hình giúp e ạ có gì giải ra ạ em cảm ơn ạ=))
vẽ hình giúp e ạ có gì giải ra ạ em cảm ơn ạ=))

a: Xet ΔBAD vuông tại A và ΔBMD vuông tại M có
BD chung
góc ABD=góc MBD
=>ΔBAD=ΔBMD
b: AD=DM
DM<DC
=>AD<CD
c: Xét ΔDAK vuông tại A và ΔDMC vuông tại M có
DA=DM
góc ADK=góc MDC
=>ΔDAK=ΔDMC
=>AK=MC: DK=DC
=>ΔDKC cân tại D; BK=BC
=>ΔBKC can tại B
mà BN là phân giác
nên BN vuông góc KC