Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔOAD và ΔOCB có
OA=OC
\(\widehat{O}\) chung
OD=OB
Do đó: ΔOAD=ΔOCB
Suy ra: AD=CB

a: Xét ΔCAD vuông tại A và ΔCED vuông tại E có
CD chung
CA=CE
Do đó:ΔCAD=ΔCED
Suy ra: DA=DE
b: Xét ΔADK vuông tại A và ΔEDB vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDB}\)
Do đó:ΔADK=ΔEDB
c: AB=8cm

3:
a: AB<AC<BC
=>góc C<góc B<góc A
b: Xét ΔDCB có
CA,DK là trung tuyến
CA cắt DK tại M
=>M là trọng tâm
=>CM=2/3*8=16/3cm
c: Gọi H là trung điểm của AC
=>HQ//AD(HQ vuông góc AC)
mà H là trung điểm của AC
nên Q là trung điểm của CD
=>B,M,Q thẳng hàng


a: EG=căn 15^2-12^2=9cm
b: Xét ΔDEH vuông tại E và ΔDIH vuông tại I có
DH chung
góc EDH=góc IDH
=>ΔDEH=ΔDIH
=>HE=HI
c: Xét ΔHEP vuông tại E và ΔHIG vuông tại I có
HE=HI
góc EHP=góc IHG
=>ΔHEP=ΔHIG
=>HP=HG
d: HE=HI
HI<HG
=>HE<HG
e: DE+EP=DP
DI+IG=DG
mà DE=DI và EP=IG
nên DP=DG
mà HP=HG
nên DH là trung trực của PG
=>D,H,A thẳng hàng

Câu 3:
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
Suy ra:HB=HC
b: Ta có: ΔAHB=ΔAHC
nên \(\widehat{BAH}=\widehat{CAH}\)
c: Ta có:ΔABC cân tại A
mà AH là đường cao
nên AH là tia phân giác của góc BAC

a: góc xOt=góc yOt=100/2=50 độ
b: góc xOt'=180 độ-góc xOt=130 độ

a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
=>AD=ED
b: Xét ΔBEF vuông tại E và ΔBAC vuông tại A có
BE=BA
góc EBF chung
=>ΔBEF=ΔBAC
=>BF=BC
2BF=BF+BC>FC

ΔAED vuông tại E nên AE<AD
ΔDFC vuông tại F nên FC<DC
=>AE+FC<AD+DC=AC
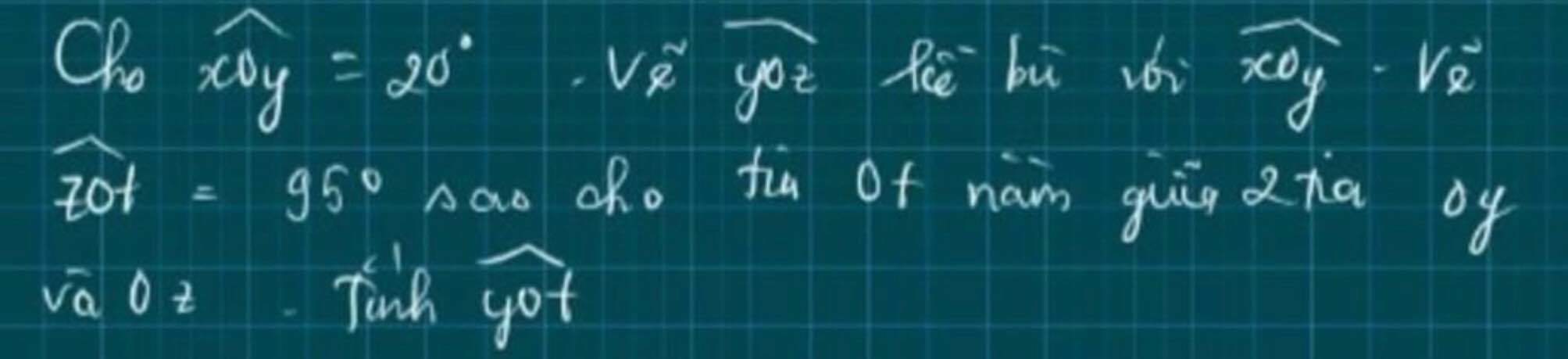

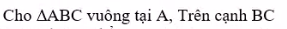


 vẽ hình luôn giúp em ạ
vẽ hình luôn giúp em ạ



 Giúp dùm mik câu b với ạ!! Vẽ hình câu b giúp mik luôn nhé
Giúp dùm mik câu b với ạ!! Vẽ hình câu b giúp mik luôn nhé