Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

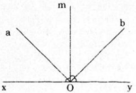
+ Trên cùng một nửa mặt phẳng bờ xy chứa tia Om có Om là tia nằm giữa tia Oa và tia Ob.
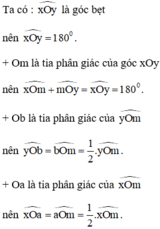
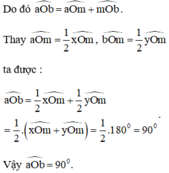

giải:
Cách 1. Giải tương tự bài 34 ta được = 900
Cách 2. Tia Oa là tia phân giác của góc xOm nên aOm=
Tia Ob là tia phân giác của góc yOm nên bOm= .
Tia Om nằm giữa hai tia Oa, Ob do đó: =
+
= 900

Vì tia \(Om\) là tia phân giác của góc \(\widehat{xoy}\)nên:
Ta có: \(\widehat{xOm}\)\(=\)\(\widehat{yOm}\)\(=\)\(\frac{\widehat{xOy}}{2}\) \(=\)\(\frac{180^0}{2}\)\(=\)\(90^0\)
Vì tia \(Oa\)là tia phân giác của góc \(\widehat{xOm}\)nên:
Ta có: \(\widehat{xOa}\) \(=\)\(\widehat{aOm}\)\(=\)\(\frac{\widehat{xOm}}{2}\)\(=\) \(\frac{90^0}{2}\) \(=\)\(45^0\) \(\left(1\right)\)
Vì tia \(Ob\)là tia phân giác của góc \(\widehat{yOm}\)nên:
Ta có: \(\widehat{yOb}\) \(=\) \(\widehat{bOm}\)\(=\)\(\frac{\widehat{yOm}}{2}\)\(=\) \(\frac{90^0}{2}\) \(=\)\(45^0\) \(\left(2\right)\)
Từ \(\left(1\right)\)và \(\left(2\right)\)ta có:
\(\widehat{aOm}\)\(+\)\(\widehat{bOm}\)\(=\)\(\widehat{aOb}\)
\(45^0\) \(+\)\(45^0\) \(=\)\(\widehat{aOb}\)
\(90^0\) \(=\)\(\widehat{aOb}\)
Vậy góc \(\widehat{aOb}\)có số đo là \(90^0\)