Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

số đường thẳng tạo bởi n điểm ( không có 3 điểm nào thẳng hàng ) là : n(n-1):2
ta có : n(n-1):2 =55 => n(n-1) = 110 = 11. (11-1) => n =11
Vậy có 11 điêrm
Ta có : \(\frac{n\left(n-1\right)}{2}=55\)( đường thẳng )
\(\Rightarrow n\left(n-1\right)=55.2\)( đường thẳng )
\(n\left(n-1\right)=110\)( đường thẳng )
\(\Rightarrow n=11\)

Số điểm còn lại là 40 - 10 = 30
Ta có : Lấy một điểm bất kì ta vẽ được 29 đường thẳng
=> trong 30 điểm đó ta vẽ được (30 . 29) : 2 = 435 đường thẳng
10 điểm còn lại vì qua hai điểm mới vẽ được 1 đường thẳng
=> lấy 1 điểm bất kì vẽ được 10 - 1 = 9 đường thẳng
=> 10 điểm còn lại vẽ được 10 . 9 : 2 = 45 đường thẳng
=> 40 điểm đó ta vẽ được 45 + 435 = 480 đường thẳng

Câu đúng: a) và g).
Câu sai: b), c), d), e), f), h).
Giải thích:
- Câu b sai vì nếu ba điểm( phân biệt) cho trước là ba điểm thẳng hàng thì có đúng 1 đường thẳng đi qua ba điểm đó.
- Câu c sai vì nếu bốn điểm ( phân biệt) cho trước là bốn điểm thẳng hàng thì có đúng 1 đường thẳng đi qua bốn điểm đó.
- Câu d sai vì hai đường thẳng phân biệt có thể song song hoặc cắt nhau.
- Câu e sai vì hai đường thẳng không cắt nhau có thể trùng nhau hoặc song song.
- Câu f sai vì hai đường thẳng không song song có thể có thể trùng nhau hoặc cắt nhau.
- Câu h sai vì ba đường thẳng phân biệt, đôi một cắt nhau thì có thể có đúng 1 giao điểm. Như hình vẽ dưới đây.
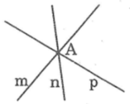
Có 8 giao điểm