Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp: Thay t vào phương trình của li độ và vận tốc
Cách giải:
Biểu thức vận tốc v = 40πcos(10πt + 5π/6) cm/s
Thay t = 0,5s ta được x = -2cm, v = 20π 3 cm/s

Đáp án B
Phương pháp: Thay t vào phương trình li độ và vận tốc
Cách giải:
Phương trình dao động của vật: x = 4cos(πt + π/4)cm → vận tốc: v = - 4πsin(πt + π/4)(cm/s)
→Tại t = 0,5s thì:
Li độ: x = 4cos(π.0,5 + π/4) = - 2 2 cm
Vận tốc:
![]()

Bài 1 :
x = -3cos(5πt - π/3) = 3cos(5πt - π/3 + π) = 3cos(5πt + 2π/3)
Biên độ A = 3(cm)
Tần số góc ω = 5π
Bài 2 :
x = 4sin(5πt - π/6) = 4cos(5πt - π/6 - π/2) = 4cos(5πt -2π/3)
Tại thời điểm t = 0,5s. Ta có :
v = -5π.4.sin(5πt - 2π/3) = -5π.4.sin(5π.0,5 - 2π/3) = 31,31(cm/s)
a = -(5π)2.4.cos(5π.0,5 - 2π/3) = -854,73(cm/s2)
Lời giài:
Bài tập số 1:
\(x=-3cos\left(5\pi t-\dfrac{\pi}{3}\right)\)
\(x=3cos\left(5\pi t+\pi-\dfrac{\pi}{3}\right)\)
\(x=3cos\left(5\pi t+\dfrac{2\pi}{3}\right)\)
Đối chiếu: \(x=3\left(5\pi t+\dfrac{2\pi}{3}\right)vớix=Acos\left(\omega t+\varphi\right)\)
\(\rightarrow\left\{{}\begin{matrix}A=3\left(cm\right)\\\omega=5\pi\left(rad/s\right)\end{matrix}\right.\)

Câu 64: Một vật dao động điều hoà trên trục x’0x với chu kỳ T = 0,5s, Gốc toạ độ O là vị trí cân bằng của vật. Lúc t = 0 vât đi qua vị trí có li độ x = 3 cm, và vận tốc bằng 0. Phương trình dao động của vật:
A. x = 5cos(4π.t)(cm) B. x = 5cos(4π .t +π)(cm)
C. x = 3cos(4π.t +π)(cm) D. x = 3cos(4π.t)(cm)

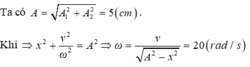
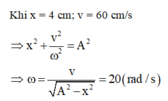
Thay t=0,5s vào phương trình li độ ta có: x=4cos(10\(\pi.0,5+\dfrac{\pi}{3}\))=-2(cm)
Ta có phương trình vận tốc của vật là: v=-40\(\pi\)sin(10\(\pi.t+\dfrac{\pi}{3}\)) (cm/s)
Thay t=0,5s vào phương trình vận tốc ta có: v=-40\(\pi\)sin(10\(\pi.0,5+\dfrac{\pi}{3}\))=\(20\sqrt{3}\pi\) (cm/s)