Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(R_{12}=\dfrac{15.30}{15+30}=10\left(\Omega\right)\)
\(R_m=R_{12}+R_3=10+30=40\left(\Omega\right)\)
\(I_m=\dfrac{U_{AB}}{R_m}=\dfrac{12}{40}=0,3\left(A\right)\)
\(b,I_{12}=I_3=0,3\left(A\right)\)
\(\dfrac{I_1}{I_2}=\dfrac{R_2}{R_1}=\dfrac{30}{15}=\dfrac{2}{1}\)
\(\rightarrow I_1=0,2\left(A\right);I_2=0,1\left(A\right)\)

\(a,R_{23}=R_2+R_3=30+30=60\left(\Omega\right)\)
\(R_m=\dfrac{R_{23}.R_1}{R_{23}+R_1}=\dfrac{60.15}{60+15}=12\left(\Omega\right)\)
\(b,I_m=\dfrac{U_{AB}}{R_m}=\dfrac{12}{12}=1\left(A\right)\)
\(I_1+I_{23}=1\left(A\right)\)
\(\dfrac{I_1}{I_{23}}=\dfrac{R_{23}}{R_1}=\dfrac{60}{15}=\dfrac{4}{1}\)
\(\rightarrow I_1=0,8\left(A\right);I_{23}=0,2\left(A\right)\)
\(\rightarrow I_2=I_3=0,2\left(A\right)\)

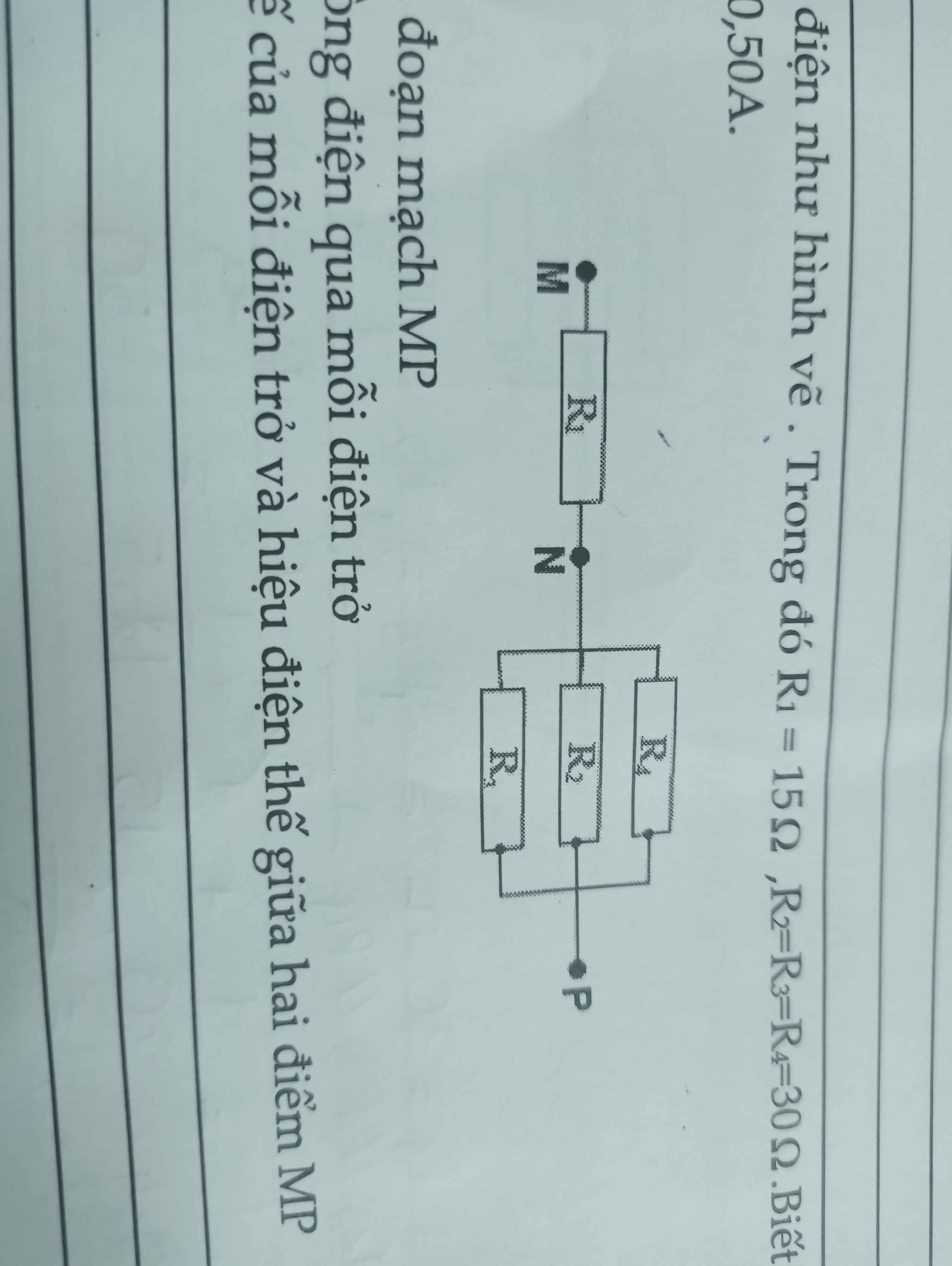
R1 n t (R2//R3//R4)
a,\(=>\dfrac{1}{R234}=\dfrac{1}{R2}+\dfrac{1}{R3}+\dfrac{1}{R4}=>R234=10\left(om\right)\)
\(=>Rmp=R1+R234=25\left(ôm\right)\)
b
ta thấy R2=R3=R4 mà U2=U3=U4
=>I2=I3=I4=0,5A
\(=>I1=I2+I3+I4=1,5A\)
c,\(U2=U3=U4=I2.R2=15V\)
\(U1=I1.R1=22,5V=>Ump=U1+U2=37,5V\)

R1nt(R2//R3)
a) \(R_{23}=\dfrac{R_2.R_3}{R_2+R_3}=2\left(\Omega\right)\)
\(\rightarrow R_{td}=R_1+R_{23}=4+2=6\left(\Omega\right)\)
b) Ta có : \(I_1=I_{23}=I=\dfrac{U}{R_{tđ}}=\dfrac{6}{2}=3A\)
\(U_{23}=U_2=U_3=I_{23}.R_{23}=3.2=6V\)
\(\rightarrow I_2=\dfrac{U_2}{R_2}=\dfrac{6}{6}=1A\)

\(R_{23}=\dfrac{R_2.R_3}{R_2+R_3}=\dfrac{10.15}{10+15}=6\left(\Omega\right)\)
\(R_{tđ}=R_1+R_{23}=9+6=15\left(\Omega\right)\)
\(I=I_1=I_{23}=\dfrac{U}{R_{tđ}}=\dfrac{27}{15}=1,8\left(A\right)\)
\(U_{23}=U_2=U_3=I_{23}.R_{23}=1,8.6=10,8\left(V\right)\)
\(\left\{{}\begin{matrix}I_2=\dfrac{U_2}{R_2}=\dfrac{10,8}{10}=1,08\left(A\right)\\I_3=\dfrac{U_3}{R_3}=\dfrac{10,8}{15}=0,72\left(A\right)\end{matrix}\right.\)
\(R_{23}=\dfrac{R_2\cdot R_3}{R_2+R_3}=\dfrac{10\cdot15}{10+15}=6\Omega\)
\(R_m=R_1+R_{23}=R_1+\dfrac{R_2R_3}{R_2\cdot R_3}=9+\dfrac{10\cdot15}{10+15}=15\Omega\)
\(I_1=I_{23}=I_m=\dfrac{U}{R}=\dfrac{27}{15}=1,8A\)
\(U_2=U_3=U_{23}=I_{23}\cdot R_{23}=6\cdot1,8=10,8V\)
\(\Rightarrow\) \(I_2=\dfrac{U_2}{R_2}=\dfrac{10,8}{10}=1,08A\)
\(I_3=\dfrac{U_3}{R_3}=\dfrac{10,8}{15}=0,72A\)
Ta có :R12=R1+R2=10+10=20\(\Omega\)
Có :(R1nt R2)//R3 :
\(\Rightarrow\)R123=\(\frac{R_{12}.R_3}{R_{12}+R_3}=\frac{20.5}{20+5}=4\Omega\)
Có : R4nt(R1ntR2)//R3):
\(\Rightarrow\)Rtđ=R4+R123=6+4=10\(\Omega\)
\(\Rightarrow\)Ic=\(\frac{U}{R_{tđ}}=\frac{12}{10}=1,2A\)
\(\Rightarrow\)Ic=I4=I123=1,2A
\(\Rightarrow\)U4=I4.R4=1,2.6=7,2V
Có :R4nt((R1ntR2)//R3)
\(\Rightarrow\)U=U4+U123
\(\Rightarrow\)U123=U-U4=12-7,2=4,8V
mà (R1ntR2)//R3
\(\Rightarrow\)U12=U3=U123=4,8V
\(\Rightarrow\)I12=\(\frac{U_{12}}{R_{12}}=\frac{4,8}{20}=0,24A\)\(\Rightarrow\)I1=I2=I12=0,24A\(\Rightarrow\)\(\left\{{}\begin{matrix}U_1=R_1.I_1=10.0,24=2,4V\\U_2=R_2.I_2=10.0,24=2,4V\end{matrix}\right.\)
\(\Rightarrow\) I3=\(\frac{U_3}{R_3}=\frac{4,8}{5}=0,96\)A