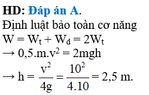Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cơ năng ban đầu:
\(W=\dfrac{1}{2}mv^2+mgh=10m\cdot h\left(J\right)\)
Cơ năng tại nơi \(W_đ=5W_t\Rightarrow W_t=\dfrac{1}{5}W_đ\):
\(W'=\dfrac{1}{2}mv^2+mgz=\dfrac{1}{2}\cdot m\cdot5^2+\dfrac{1}{5}\cdot\dfrac{1}{2}\cdot m\cdot5^2=15m\left(J\right)\)
Bảo toàn cơ năng: \(W=W'\)
\(\Rightarrow10m\cdot h=15m\Rightarrow h=\dfrac{15}{10}=1,5m\)

\(m = 200g = 0,2kg\\ W_đ = \dfrac{m.v^2}{2} = \dfrac{0,2.6}{2} = 0,6(J)\\ W_t = m.g.h = 0,2.10.5 = 10 (J)\\ W = W_đ + W_t = 0,6 + 10 = 10,6 (J)\\ W_đ = W_t \\ \Rightarrow W_t = \dfrac{W}{2} = \dfrac{10,6}{2} = 5,3 (J)\\ \Rightarrow h = \dfrac{W_t}{m.g} = \dfrac{5,3}{0,2.10} = 2,65 (m)\)

Chọn gốc thế năng tại độ cao 5m so với mặt đất.
\(\Rightarrow h=10-5=5cm\)
Cơ năng vật:
\(W=\dfrac{1}{2}mv^2+mgh=\dfrac{1}{2}\cdot0,4\cdot20^2+0,4\cdot10\cdot5=100J\)
Ta có
\(W=W_đ+W_t\\ \Leftrightarrow mgh+\dfrac{mv^2}{2}=0,4.10.10+\dfrac{0,4.20^2}{2}\\ =120\left(J\right)\)

Chọn mốc thế năng tại mặt đất.
Cơ năng của vật tại vị trí ném là:
W0=\(W_{đ0}\)+W0 = \(\dfrac{1}{2}mv_0^2\) + 0 = \(\dfrac{1}{2}mv_0^2\) (J)
a) Khi vật đạt độ cao cực đại, vận tốc vật là v3,21= 0 \(\Rightarrow\) \(W_{đ1}=\dfrac{1}{2}mv_1^2=0\) (J)
W1 = \(W_{đ1}+W_{t1}=0+mgh_{max}\) = mghmax (J)
Áp dụng định luật bảo toàn cơ năng: W1=W0
\(\Leftrightarrow mgh_{max}=\dfrac{1}{2}mv_0^2\Leftrightarrow10.h_{max}=\dfrac{1}{2}.8^2\)\(\Leftrightarrow h_{max}=3,2\) (m)
b) Ta có \(\left\{{}\begin{matrix}W_đ+W_t=W\\W_đ=3.W_t\end{matrix}\right.\)mà W=W0 (do cơ năng được bảo toàn) \(\Rightarrow\left\{{}\begin{matrix}W_đ=\dfrac{3}{4}W_0\\W_t=\dfrac{1}{4}W_0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{2}mv^2=\dfrac{3}{4}.\dfrac{1}{2}mv^2_0\\mgz=\dfrac{1}{4}.\dfrac{1}{2}mv^2_0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}v^2=\dfrac{3}{4}.8^2\\10.z=\dfrac{1}{4}.\dfrac{1}{2}.8^2\end{matrix}\right.\) \(\left\{{}\begin{matrix}v=4\sqrt{3}\left(\dfrac{m}{s}\right)\\z=0,8\left(m\right)\end{matrix}\right.\)
c) Ta thấy 5 > 3,2=hmax \(\rightarrow\)Sau khi đi được 5m kể từ lúc bắt đầu ném, vật cách mặt đất là :
z2 = 3,2 - ( 5- 3,2 ) = 1,4 (m)
Cơ năng của vật khi đó là W2 = \(W_{đ2}+W_{t2}=\dfrac{1}{2}mv^2_2+mgz_2\) (J)
Áp dụng định luật bảo toàn cơ năng, ta có: W2 = W0
\(\Leftrightarrow\dfrac{1}{2}mv_2^2+mgz_2=\dfrac{1}{2}mv_0^2\) \(\Leftrightarrow v_2^2+2gz_2=v_0^2\) \(\Leftrightarrow v_2^2+2.10.1,4=8^2\) \(\Rightarrow\) v2 = 6 (m/s)

a. Áp dụng ĐL bảo toàn cơ năng cho vật tại vị trí ném và mặt đất
\(\frac{1}{2}mv_0^2+mgh=\frac{1}{2}mv_{max}^2\)
\(\Rightarrow v_0^2=v_{max}^2-2gh=18^2-2.10.16=4\)
\(\Rightarrow v_0=2\) m/s
b. Tại vị trí động năng bằng thế năng có
\(W=2W_t\)
\(\Rightarrow\frac{1}{2}mv_{max}^2=2mgh\)
\(\Rightarrow h=\frac{1}{4g}v_{max}^2=8,1\) m

a, \(W_đ=\dfrac{1}{2}mv^2=\dfrac{1}{2}\cdot0,1\cdot5^2=1,25\left(J\right)\)
\(W_t=mgz=0,1\cdot10\cdot2=2\left(J\right)\)
\(W=W_đ+W_t=1,25+2=3,25\left(J\right)\)
b, Gọi vị trí 1 là vị trí vật đạt được độ cao cực đại
Khi vật đạt được độ cao cực đại z1 thì v1 = 0
\(W_1=W_{đ_1}+W_{t_1}=\dfrac{1}{2}mv_1^2+mgz_1=mgz_1\)
Áp dụng ĐLBTCN: \(W=W_1\Leftrightarrow W=mgz_1\Leftrightarrow z_1=\dfrac{W}{mg}=\dfrac{3,25}{0,1\cdot10}=3,25\left(m\right)\)