Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số đo góc ngoài tại đỉnh \(D\) là: \(360^\circ - \left( {65^\circ + 100^\circ + 60^\circ } \right) = 135^\circ \)

Đề bài có chút nhầm lẫn, hình như góc ngoài đỉnh D = 115º?
+ Góc ngoài đỉnh B = 75º (gt) => góc B = 180º - 75º = 105º
+ Góc ngoài đỉnh D = 115º (gt) => góc D = 180º - 115º = 65º
+ Tứ giác ABCD có:
góc A + góc B + góc C + góc D = 360º
=> 90º + 105º + góc C + 65º = 360º
=> góc C + 260º = 360º
=> góc C = 100º
Vậy, góc C = 100º

Ta có: ˆA+ˆB+ˆC+ˆD=360oA^+B^+C^+D^=360o
⇒ˆA+120độ+60độ+90độ=360độ⇒A^+120độ+60độ+90độ=360độ
⇒ˆA=360độ−90độ−60độ−120độ=90 độ

Gọi góc ngoài đỉnh B là x
Ta có:
$\widehat {B} + x = 180^0 $
`=>`$ \widehat {B} + 110^0 = 180^0$
`=>` $\widehat {B} = 70^0$
Xét tứ giác ABCD:
$\widehat {A} + \widehat {B} + \widehat {C} + \widehat {D}= 360^0$
`=>` $100^0 + 70^0 + 75^0 + \widehat {D} = 360^0$
`=>` $\widehat {D} = 115^0$
Vậy, $\widehat {D} = 115^0.$

Số đo góc ngoài tại đỉnh B là:
\(180^0-360^0+57^0+110^0+75^0=62^0\)

Đáp án cần chọn là: C
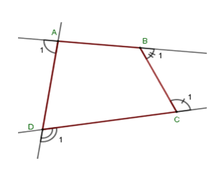
Gọi góc ngoài tại 4 đỉnh A, B, C, D của tứ giác ABCD lần lượt là A 1 ^ ; B 1 ^ ; C 1 ^ ; D 1 ^ .
Khi đó ta có :
A ^ + A 1 ^ = 180 ° ⇒ A 1 ^ = 180 ° - A ^ ;
Theo kết quả các câu trước ta có
A 1 ^ + B 1 ^ + C 1 ^ + D 1 ^ = 360 ° ⇒ B 1 ^ + C 1 ^ + D 1 ^ = 360 ° - A ^ = 360 ° - 80 ° = 280 °
Vậy B 1 ^ + C 1 ^ + D 1 ^ = 280 °

Ta có :
\(\widehat{BCD}+120^o=180^o\)( kề bù )
\(\widehat{BCD}=180^o-120^o\)
\(\widehat{BCD}=60^o\)
Tứ giác ABCD có :
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
\(130^o+90^o+60^o+\widehat{D}=360^o\)
\(280^o+\widehat{D}=360^o\)
\(\widehat{D}=360^o-280^o\)
\(\widehat{D}=80^o\)

Ta có : \(^{\widehat{C_1}+\widehat{C_2}=180^o}\)(hai góc kề bù)
Mà \(\widehat{C_2}=120^o\)(gt)
Suy ra : \(\widehat{C_1}=180^o-120^o=60^o\)
Lại có : \(\widehat{A}+\widehat{B}+\widehat{C_1}+\widehat{D}=360^o\) (tổng bốn góc trong 1 tứ giác)
Mà \(\widehat{A}=130^o;\widehat{B}=90^o;\widehat{C}=60^o\)
Nên : \(\widehat{D}=360^o-130^o-90^o-60^o=80^o\)

Ta có : \(\widehat{C_1}+\widehat{C_2}=180^0\)
\(108^0+\widehat{C_2}=180^0\)
\(\widehat{C_2}=72\)
Xét tứ giác \(ABCD\) có :
\(\widehat{A}+\widehat{B}+\widehat{C_2}+\widehat{D}=360^0\)
\(\Rightarrow103^0+105^0+72^0+\widehat{D}=360^0\)
\(\Rightarrow\widehat{D}=80^0\)
Vây \(\widehat{D}=80^0\)
tính chất : tổng các góc ngoài của tứ giác bằng \(360^0\)
TRong tứ giác ABCD có các góc ngoài bằng :
góc ngoài đỉnh A + góc ngoài đỉnh B + góc ngoài đỉnh C + góc ngoài đỉnh D = 360
=> góc ngoài đỉnh D =\(360^0-(65^0+100^0+60^0)=360^0-225^0=135^0\)
kết luận góc ngoài đỉnh D = 135^0