Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc KOA+góc BOA=90 độ
góc KAO+góc COA=90 độ
mà góc BOA=góc COA
nên góc KOA=góc KAO
=>ΔKAO cân tại K
b: Xét ΔOBA vuông tại B có sin BAO=OB/OA=1/2
nên góc BAO=30 độ
=>góc BOA=60 độ
Xét ΔOBI có OB=OI và góc BOI=60 độ
nên ΔOBI đều
=>OI=OB=1/2OA=R
=>I là trung điểm của OA
ΔKAO cân tại K
mà KI là trung tuyến
nên KI vuông góc với OI
=>KI là tiếp tuyến của (O)

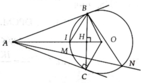
a, A B M ^ = A N B ^ = 1 2 s đ B M ⏜
Chứng minh được: ∆ABM:∆ANB (g.g) => ĐPCM
b, Chứng minh AO ^ BC áp dụng hệ thức lượng trong tam giác vuông ABO và sử dụng kết quả câu a) Þ AB2 = AH.AO
c, Chứng minh được A B I ^ = C B I ^ B I ⏜ = C I ⏜ => BI là phân giác A B C ^ . Mà AO là tia phân giác B A C ^ => I là tâm đường tròn nội tiếp ∆ABC

a: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra AO là đường trung trực của BC
b: AO là đường trung trực của BC
=>AO\(\perp\)BC tại H và H là trung điểm của BC
Xét (O) có
\(\widehat{ABE}\) là góc tạo bởi tiếp tuyến BA và dây cung BE
\(\widehat{EDB}\) là góc nội tiếp chắn cung BE
Do đó: \(\widehat{ABE}=\widehat{EDB}\)
Xét ΔABE và ΔADB có
\(\widehat{ABE}=\widehat{ADB}\)
\(\widehat{BAE}\) chung
Do đó: ΔABE đồng dạng với ΔADB
=>\(\dfrac{AB}{AD}=\dfrac{AE}{AB}\)
=>\(AB^2=AD\cdot AE\)
c: Xét (O) có
MB,ME là các tiếp tuyến
Do đó: MB=ME
Xét (O) có
NE,NC là các tiếp tuyến
Do đó: NE=NC
Chu vi tam giác AMN là:
\(AM+MN+AN\)
\(=AM+ME+EN+AN\)
\(=AM+MB+AN+NC\)
=AB+AC
Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
hay A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
=>AI là đường trung trực của BC
=>IB=IC