Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xet ΔABD và ΔAEB có
góc ABD=góc AEB
góc BAD chung
=>ΔABD đồng dạngvới ΔAEB
=>AB/AE=AD/AB
=>AB^2=AD*AE
b: Xét (O) có
AB,AC là tiếp tuyến
=>AB=AC
mà OB=OC
nên OA là trung trực của BC
=>OA vuông góc BC
=>AH*AO=AB^2=AD*AE
=>AH/AE=AD/AO
=>ΔAHD đồng dạng với ΔAEO
=>góc AHD=góc AEO
=>góc OHD+góc OED=180 độ
=>OHDE nội tiếp

a: Xét tứ giác OIBA có \(\widehat{OIA}=\widehat{OBA}=90^0\)
nên OIBA là tứ giác nội tiếp
b: Xét ΔACD và ΔAEC có
\(\widehat{ACD}=\widehat{AEC}\)
\(\widehat{DAC}\) chung
Do đó: ΔACD\(\sim\)ΔAEC
SUy ra: AC/AE=AD/AC
hay \(AC^2=AE\cdot AD\left(1\right)\)
c: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
mà OB=OC
nên OA là đường trung trực của BC
Xét ΔOCA vuông tại C có CK là đường cao
nên \(AK\cdot AO=AC^2\left(2\right)\)
Từ (1) và (2) suy ra \(AK\cdot AO=AD\cdot AE\)
hay AK/AE=AD/AO
Xét ΔAKD và ΔAEO có
AK/AE=AD/AO
góc KAD chung
DO đó: ΔAKD\(\sim\)ΔAEO
Suy ra: \(\widehat{AKD}=\widehat{AEO}\)

a) Vì AB,AC là tiếp tuyến \(\Rightarrow\Delta ABC\) cân tại A có AO là phân giác \(\angle BAC\)
\(\Rightarrow OA\bot BC\)
Xét \(\Delta ABD\) và \(\Delta AEB:\) Ta có: \(\left\{{}\begin{matrix}\angle ABD=\angle AEB\\\angle EABchung\end{matrix}\right.\)
\(\Rightarrow\Delta ABD\sim\Delta AEB\left(g-g\right)\Rightarrow\dfrac{AB}{AE}=\dfrac{AD}{AB}\Rightarrow AB^2=AD.AE\)
b) tam giác ABO vuông tại B có đường cao BH nên áp dụng hệ thức lượng
\(\Rightarrow AB^2=AH.AO\Rightarrow AH.AO=AD.AE\Rightarrow\dfrac{AH}{AE}=\dfrac{AD}{AO}\)
Xét \(\Delta AHD\) và \(\Delta AEO:\) Ta có: \(\left\{{}\begin{matrix}\dfrac{AH}{AE}=\dfrac{AD}{AO}\\\angle EAOchung\end{matrix}\right.\)
\(\Rightarrow\Delta AHD\sim\Delta AEO\left(c-g-c\right)\Rightarrow\angle AHD=\angle AEO\Rightarrow DEOH\) nội tiếp
c) Ta có: \(\angle BHE=90-\angle OHE=90-\angle ODE\) (DEOH nội tiếp)
\(=90-\dfrac{180-\angle DOE}{2}=\dfrac{1}{2}\angle DOE=\dfrac{1}{2}\angle DHE\) (DEOH nội tiếp)
\(\Rightarrow HB\) là phân giác \(\angle DHE\Rightarrow\dfrac{ID}{IE}=\dfrac{DH}{HE}\)
Vì HB là phân giác \(\angle DHE\) và \(HA\bot HB\Rightarrow HA\) là phân giác ngoài \(\angle DHE\)
\(\Rightarrow\dfrac{AD}{AE}=\dfrac{DH}{HE}=\dfrac{ID}{IE}\Rightarrow AD.IE=ID.AE\)
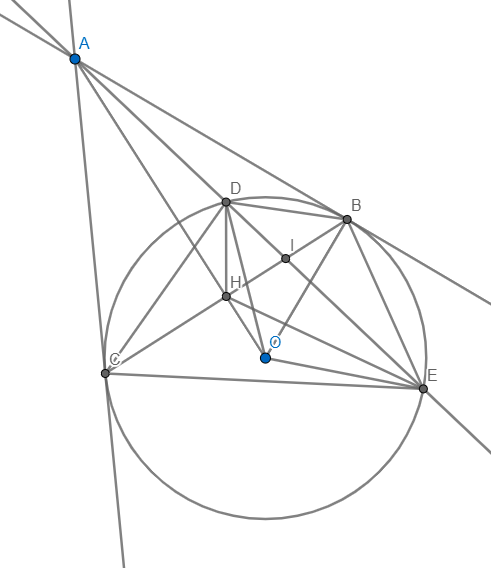
a) Xét (O) có
AB là tiếp tuyến có B là tiếp điểm(gt)
AC là tiếp tuyến có C là tiếp điểm(gt)
Do đó: AB=AC(Tính chất hai tiếp tuyến cắt nhau)
Ta có: AB=AC(cmt)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: OB=OC(=R)
nên O nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
hay OA\(\perp\)BC tại H
Xét ΔADB và ΔABE có
\(\widehat{BAD}\) chung
\(\widehat{ABD}=\widehat{AEB}\left(=\dfrac{1}{2}sđ\stackrel\frown{BD}\right)\)
Do đó: ΔADB\(\sim\)ΔABE(g-g)
Suy ra: \(\dfrac{AD}{AB}=\dfrac{AB}{AE}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AB^2=AD\cdot AE\)

a: góc KOA+góc BOA=90 độ
góc KAO+góc COA=90 độ
mà góc BOA=góc COA
nên góc KOA=góc KAO
=>ΔKAO cân tại K
b: Xét ΔOBA vuông tại B có sin BAO=OB/OA=1/2
nên góc BAO=30 độ
=>góc BOA=60 độ
Xét ΔOBI có OB=OI và góc BOI=60 độ
nên ΔOBI đều
=>OI=OB=1/2OA=R
=>I là trung điểm của OA
ΔKAO cân tại K
mà KI là trung tuyến
nên KI vuông góc với OI
=>KI là tiếp tuyến của (O)