Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi x là số có 6 chữ số đôi một khác nhau và hai chữ số 1 và 2 luôn đứng cạnh nhau.
Đặt y=12 khi đó x có dạng 
với a;b;c;d;e đôi một khác nhau và thuộc tập {y;;3;4;5;6} nên có 5!=120 số.
Khi hoán vị hai số 1;2 ta được một số khác nên có 120.2=240 số
Vậy số thỏa yêu cầu bài toán là: 6!-240=480 số.
Chọn B.
Gọi x là số có 6 chữ số đôi một khác nhau và hai chữ số 1 và 2 luôn đứng cạnh nhau.
Đặt y=12 khi đó x có dạng 
với a;b;c;d;e đôi một khác nhau và thuộc tập {y;3;4;5;6} nên có
Khi hoán vị hai số1;2 ta được một số khác nên có 120.2=240 số x.
Vậy số thỏa yêu cầu bài toán là: P6 - 240 =480số.
Chọn B.
1.
Chữ số hàng đơn vị có 4 cách chọn (từ 1,3,5,7)
Chọn và hoán vị 4 chữ số từ 6 chữ số còn lại: \(A_6^4\) cách
Tổng cộng: \(4.A_6^4\) cách
2.
Gọi chữ số cần lập có dạng \(\overline{abcd}\)
a.
Lập số có 4 chữ số bất kì (các chữ số đôi một khác nhau): \(A_6^4\) cách
Lập số có 4 chữ số sao cho số 0 đứng đầu: \(A_5^3\) cách
\(\Rightarrow A_6^4-A_5^3=300\) số
b.
Để số được lập là số chẵn \(\Rightarrow\) d chẵn
TH1: \(d=0\Rightarrow abc\) có \(A_5^3\) cách chọn
TH2: \(d\ne0\Rightarrow d\) có 2 cách chọn (từ 2;4)
a có 4 cách chọn (khác 0 và d), b có 4 cách chọn, c có 3 cách chọn
\(\Rightarrow2.4.4.3=96\) số
Tổng cộng: \(A_5^3+96=156\) số
Xác suất \(P=\dfrac{156}{300}=...\)
Đáp án C
Số các số tự nhiên thỏa mãn yêu cầu bài toán là: A 6 4 = 360 số
Đáp án C
Chọn số tự nhiên gồm 4 chữ số trong 6 chữ số có A 6 4 = 360 cách chọn
Không biết đề là ba số đầu khác 123 hay số đầu tiên khác 1, 2, 3. Đây t làm theo cách hiểu thứ nhất nha.
Theo giả thiết, số cách sắp xếp 3 chữ số đầu tiên là \(A_8^3-1=335\)
Số cách sắp xếp 2 chữ số cuối là \(A_5^2=20\)
\(\Rightarrow\) Có \(335.20=6700\) cách lập số tự nhiên thỏa mãn yêu cầu bài toán.
Không biết đúng không nữa-.-
Đáp án D
Phương pháp: Xét từng trường hợp: chữ số đầu tiên bằng 1, chữ số thứ hai bằng 1, chữ số thứ ba bằng 1.
Cách giải: Gọi số đó là a b c d e
- TH1: a = 1
+ b có 7 cách chọn.
+ c có 6 cách chọn.
+ d có 5 cách chọn.
+ e có 4 cách chọn.
Nên có: 7.6.5.4 = 840 số
- TH2: b = 1
+ a ≠ b , a ≠ 0 , nên có 6 cách chọn.
+ c có 6 cách chọn.
+ d có 5 cách chọn.
+ e có 4 cách chọn.
Nên có: 6.6.5.4 = 720 số.
- TH3: c = 1.
+ a ≠ c , a ≠ 0 , nên có 6 cách chọn.
+ b có 6 cách chọn.
+ d có 5 cách chọn.
+ e có 4 cách chọn.
Nên có 6.6.5.4 = 720 số.
Vậy có tất cả 840 + 720 + 720 = 2280 số.
Mỗi số cần lập ứng với một chỉnh hợp chập 3 của 6 phần tử
Nên số các số thỏa mãn là: 
số.
→Đáp án C.
Gọi số cần lập là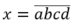
Vì a khác 1 nên a có 5 cách chọn. Ứng với mỗi cách chọn a ta có: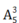
cách chọn b;c;d.
Vậy c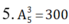ó
số .
chọn A.