Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn B
Lấy ra 3 chữ số từ 9 chữ số và sắp xếp 3 chữ số đó theo thứ tự, mỗi cách sắp xếp tạo nên 1 số có 3 chữ số khác nhau. Như vậy, có A 9 3 số cần tìm.
* Nhận xét: Mục đích bài toán là phân biệt hai khái niệm: Chỉnh hợp và tổ hợp. Học sinh có thể giải bài này bằng phương pháp nhân: 9.8.7, và so sánh với 4 đáp án. Hai chỉnh hợp khác nhau thì có thể khác nhau về phần tử hoặc khác nhau về thứ tự các phần tử. Hai tổ hợp khác nhau thì khác nhau về phần tử.
*Lý thuyết Chỉnh hợp
- Cho tập hợp A có n phần tử và cho số nguyên k, (1 ≤ k ≤ n). Khi lấy k phần tử của A và sắp xếp chúng theo một thứ tự, ta được một chỉnh hợp chập k của n phần tử của A (gọi tắt là một chỉnh hợp n chập k của A).
- Số các chỉnh hợp chập k của một tập hợp có n phần tử là: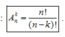 
- Một số qui ước: 
*Lý thuyết Tổ hợp
- Cho tập hợp A có n phần tử và cho số nguyên k, (1 ≤ k ≤ n). Mỗi tập hợp con của A có phần tử được gọi là một tổ hợp chập k của n phần tử của A.
- Số các chỉnh hợp chập k của một tập hợp có n phần tử là :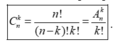 
- Một số quy ước: 
với qui ước này ta có 
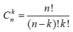đúng với số nguyên dương k, thỏa 0
≤
k
≤
n
PT 14.1. Chọn B
TH1 
TH2: 
vì 
Như vậy, có 
số cần tìm
PT 14.2.
Chọn C
Mỗi tập con có 3 phần tử thuộc tập {1,2,...,9} xác định duy nhất một số có 3 chữ số tăng dần từ trái qua phải (đảm bảo chữ số đầu tiên khác 0).
Mỗi tập con có 3 phần tử thuộc tập {0,1,2....,9} xác định duy nhất một số có 3 chữ số giảm dần từ trái qua phải.
Như vậy, có 
số cần tìm.
Gọi các số thỏa mãn đề là \(\overline{abcdef}\) (đôi một khác nhau)
- Số 7 có thể ở cả 6 vị trí.
+ Nếu a=7 => Số cách chọn các số còn lại: 9.8.7.6.5=15120 (cách)
+ Nếu a\(\ne\) 7 => Số cách chọn các số còn lại: 8.9.8.7.6.5=120960(cách)
=> Số số tự nhiên thỏa mãn: 15120+120960=136080(số)
Gọi chữ số cần lập là \(\overline{abcdef}\)
TH1: có mặt chữ số 0
Chọn 4 chữ số còn lại (ngoài 2 số 0 và 7): \(C_6^4=15\) cách
Hoán vị 6 chữ số: \(6!-5!=600\) cách
\(\Rightarrow15.600=9000\) số
TH2: không có mặt chữ số 0
Chọn 5 chữ số còn lại: \(C_6^5=6\) cách
Hoán vị 6 chữ số: \(6!=720\) cách
\(\Rightarrow6.720=4320\) số
Vậy có: \(9000+4320=13320\) số thỏa mãn
Ta có 
nên d ∈ {2;4;6;8}
·Với d=4; c=5, chọn a có 7 cách, chọn b có 6 cách nên có 7.6= 42 số thỏa mãn.
· Với d=2
1. Số cần lập có dạng 
chọn c có 6 cách nên có 6 số thỏa mãn.
2. Số cần lập có dạng 
chọn c có 6 cách nên có 6 số thỏa mãn
3. Số cần lập có dạng 
chọn a có 6 cách nên có 6 số thỏa mãn.
4. Số cần lập có dạng 
chọn a có 6 cách nên có 6 số thỏa mãn.
Như vậy với d=2 có 6+6+6+6=24 số thỏa mãn.
· Tương tự với d=6; d=8
Vậy có tất cả 42+3.24=114 số thỏa mãn.
Chọn B.
a. Gọi chữ số cần lập là \(\overline{abcd}\)
TH1: \(d=0\Rightarrow\) bộ abc có \(A_9^3\) cách chọn
TH2: \(d\ne0\Rightarrow d\) có 4 cách chọn (từ 2,4,6,8)
a có 8 cách chọn (khác 0 và d), b có 8 cách chọn (khác a và d), c có 7 cách chọn (khác a,b,d)
\(\Rightarrow4.8.8.7\) số
Tổng cộng: \(A_9^3+4.8.8.7=...\)
b. Chọn 4 chữ số còn lại: có \(C_7^4\) cách
Hoán vị 3 chữ số 0,1,2: có \(3!\) cách
Coi bộ 3 chữ số này là 1 số, hoán vị với 4 chữ số còn lại: \(5!\) cách
Ta đi tính số trường hợp 0 đứng đầu:
Số 0 đứng đầu trong bộ 0,1,2: có \(2!\) cách
Đặt bộ 0,1,2 đứng đầu, xếp vị trí cho 4 chữ số còn lại: \(4!\) cách
Vậy có: \(C_7^4.\left(3!.5!-2!.4!\right)=...\) số
a. Gọi số đó là \(\overline{ab}\)
a có 5 cách chọn (khác 0), b có 5 cách chọn (khác a)
Theo quy tắc nhân ta có: \(5.5=25\) số
b. Gọi số đó là \(\overline{abc}\)
a có 5 cách chọn (khác 0), b có 5 cách chọn (khác a), c có 4 cách chọn (khác a và b)
Có: \(5.5.4=100\) số
c. Gọi số đó là \(\overline{abcd}\)
Do số chẵn nên d chẵn
- TH1: \(d=0\) (1 cách chọn d)
a có 5 cách chọn (khác d), b có 4 cách chọn (khác a và d), c có 3 cách chọn
\(\Rightarrow1.5.4.3=60\) số
- TH2: \(d\ne0\Rightarrow d\) có 2 cách chọn (2 và 4)
a có 4 cách chọn (khác 0 và d), b có 4 cách chọn (khác a và d), c có 3 cách chọn
\(\Rightarrow2.4.4.3=96\) số
Theo quy tắc cộng, có: \(60+96=156\) số thỏa mãn
d.
Gọi số đó là \(\overline{abcde}\)
Số lẻ nên e lẻ \(\Rightarrow\) e có 3 cách chọn (1;3;5)
a có 4 cách chọn (khác 0 và e), b có 4 cách chọn (khác a và e), c có 3 cách, d có 2 cách
\(\Rightarrow3.4.4.3.2=288\) số
Chọn B
Gọi số cần tìm có dạng là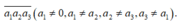
Mỗi bộ ba số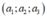
là một chỉnh hợp chập 3 của 9 phần tử.
Vậy số các số cần tìm là A 9 3 số.