Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
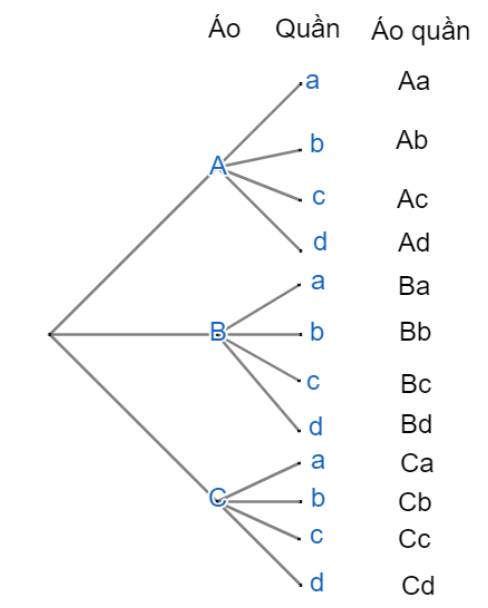
b) An có 12 cách chọn một bộ quần áo
vì: Để chọn một bộ quần áo bao gồm chọn quần riêng và áo riêng
Có 3 cách chọn một chiếc áo
Vì 4 cái quần khác nhau nên với mỗi cái áo riêng thì sẽ có 4 cách chọn 1 cái quần để tạo thành một bộ quần áo
Tương tự như vậy với hai cái áo còn lại, nên tổng cộng sẽ có 12 cách chọn một bộ quần áo (hay nhìn vào sơ đồ ta thấy rằng có 12 bộ quần áo)

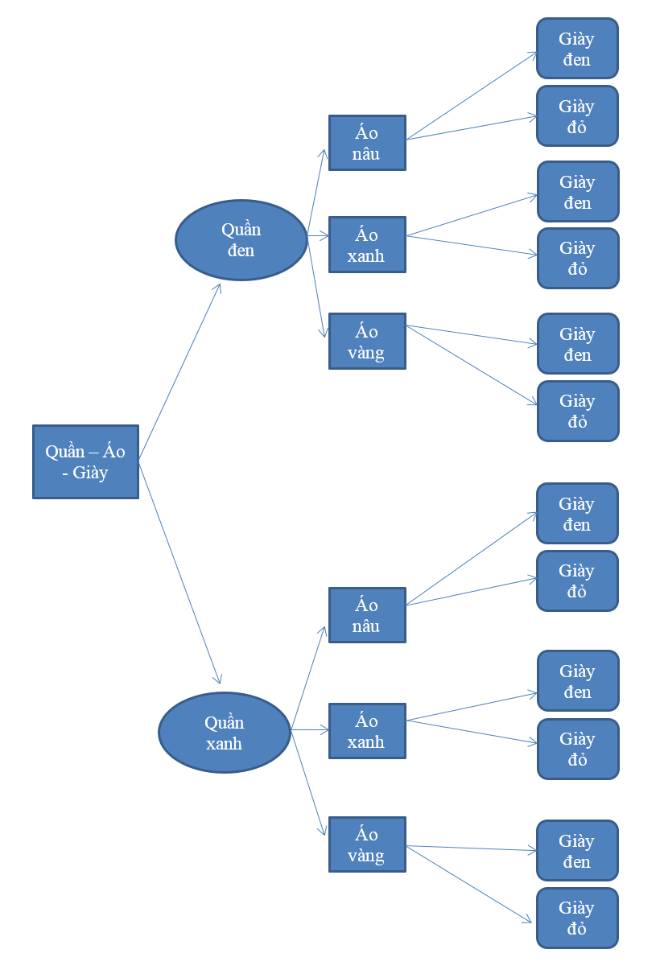
Kết luận: Từ sơ đồ cây, ta thấy bạn Dương có 12 cách chọn một bộ quần áo và một đôi giày.

Như hpt lớp 8.
Gọi giá bán áo là x , giá bán quần là y, giá bán váy là z.
Theo đề bài ta có :
\(\left\{{}\begin{matrix}12x+21y+18z=5349000\\16x+24y+12z=5600000\\24x+15y+12z=5259000\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=98000\\y=125000\\z=86000\end{matrix}\right.\)
Vậy giá bán áo là 98000 đồng, giá bán quần là 125000 đồng, giá bán váy là 86000 đồng.
Gọi giá tiền mỗi cái áo là \(x\) (đồng), giá tiền mỗi cái quần là \(y\) (đồng), giá tiền mỗi cái váy là \(z\) (đồng)
ĐK : \(x,y,z\in N^{\circledast}\)
Vì ngày thứ nhất bán được 12 áo, 21 quần và 18 váy, doanh thu 5 349 000 đồng nên
ta có phương trình : \(12x+21y+18z=5349000\) (1)
Vì ngày thứ hai bán được 16 áo, 24 quần và 12 váy, doanh thu 5 600 000 đồng nên
ta có phương trình : \(16x+24y+12z=5600000\) (2)
Vì ngày thứ ba bán được 24 áo, 15 quần và 12 váy, doanh thu 5 259 000 đồng nên
ta có phương trình : \(24x+15y+12z=5259000\) (3)
Từ (1),(2) và (3) ta có hệ phương trình :
\(\left\{{}\begin{matrix}12x+21y+18z=5349000\\16x+24y+12z=5600000\\24x+15y+12z=5259000\end{matrix}\right.\)
Giải hệ phương trình : \(\left\{{}\begin{matrix}12x+21y+18z=5349000\\16x+24y+12z=5600000\\24x+15y+12z=5259000\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=98000\left(TM\right)\\y=125000\left(TM\right)\\z=86000\left(TM\right)\end{matrix}\right.\)
Vậy giá tiền mỗi cái áo là 98000 đồng, giá tiền mỗi cái quần là 125000, giá tiền mỗi cái váy là 86000 đồng

Gọi x, y, z (đồng) lần lượt là giá tiền mỗi áo, quần và váy (0 < x, y, z < 5259000).
Ngày thứ nhất bán được 21 áo, 21 quần và 18 váy, doanh thu là 5.349.000 đồng nên ta có:
12x + 21y + 18z = 5.349.000
Ngày thứ hai bán được 16 áo, 24 quần và 12 váy, doanh thu là 5.600.000 đồng nên ta có:
16x + 24y + 12z = 5.600.000
Ngày thứ ba bán được 24 áo, 15 quần và 12 váy, doanh thu là 5.259.000 đồng nên ta có:
24x + 15y + 12z = 5.259.000
Từ đó ta có hệ phương trình:
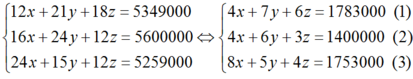
Lấy (1) – (2) ta được : y + 3z = 383000.
Nhân 2 vào hai vế của (1) rồi trừ đi (3) ta được: 9y + 8z = 1813000
Ta có hệ phương trình:
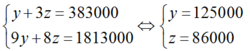
Thay y = 125000, z = 86000 vào (1) ta được x = 98000.
Vậy: Giá bán mỗi áo là: 98.000 đồng.
Giá bán mỗi quần là: 125.000 đồng.
Giá bán mỗi váy là: 86.000 đồng.

+) Số cách chọn 3 kí tự đầu tiên là 3 chữ cái trong bảng gồm 26 chữ cái in thường là: \(A_{26}^3\) (cách)
+) Số cách chọn 5 kí tự tiếp theo là chữ số là: \(A_{10}^5\) (cách)
+) Áp dụng quy tắc nhân, số mật khẩu Việt có thể tạo ra là: \(A_{26}^3.A_{10}^5\)(mật khẩu)

Khi Hannah lấy một chiếc kẹo ở lần đầu tiên, có 6/n xác suất cô lấy phải chiếc kẹo màu cam.
Bởi vì có 6 chiếc kẹo màu cam trong tổng số n chiếc kẹo.
Khi Hannah lấy một chiếc kẹo nữa ở lần thứ 2, có 5/(n-1) xác suất cô lấy phải chiếc kẹo màu cam.
Bởi vì chỉ còn 5 chiếc kẹo màu cam trong tổng số n-1 chiếc kẹo.
Xác suất lấy được 2 chiếc kẹo màu cam trong 2 lần chính là xác suất lần đầu nhân với xác suất lần thứ hai. (Đó cũng chính là kiến thức quan trọng nhất ta học được từ bài toán này).
Như vậy ta có, xác suất lấy được 2 chiếc kẹo màu cam là 6/n x 5/n-1
Mà đề bài cho dữ liệu xác suất Hannah lấy được 2 chiếc kẹo màu cam là 1/3.
Nên: 6/n x 5/n-1 = 1/3
Đến đây, tất cả những gì cần làm là rút gọn lại phương trình này.
(6x5)/n(n-1) = 30/(n2 – n) = 1/3
Hay 90/(n2 – n) = 1
Vậy (n2 – n) = 90
Suy ra: n2 – n – 90 = 0

a) Mỗi phần tử của không gian mẫu là một tổ hợp chập 2 của 20 phần tử. Do đó, số phần tử của không gian mẫu là: \(n\left( \Omega \right) = C_{20}^2\) ( phần tử)
b) Gọi A là biến cố “Tích các số trên hai thẻ là số lẻ”
Để tích các số trên thẻ là số lẻ thì cả hai thẻ bốc được đểu phải là số lẻ vậy nên ta phải chọn ngẫu nhiên 2 thẻ từ 10 thẻ số lẻ. Do đó, số phần tử các kết quả thuận lợi cho biến cố A là tổ hợp chập 2 của 10 phần tử: \(n\left( A \right) = C_{10}^2\) ( phần tử)
Vậy xác suất của biến cố A là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{C_{10}^2}}{{C_{20}^2}} = \frac{9}{{38}}\)
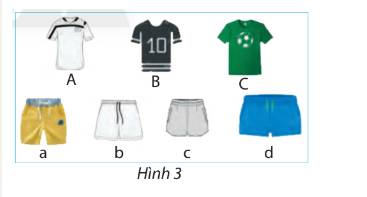
a: SỐ cách chọn là 4+3=7 cách
b: Số cách chọn là 4*3=12 cách