Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Tại M là vị trí của vân sáng bậc k
⇒ x M = k λ D a ⇒ a = k λ D x M
Thay đổi a một lượng nên ta có:
x M = k 1 . D λ a + Δ a ⇒ a + Δ a = k 1 λ D x M
Và x M = k 2 . D λ a − Δ a ⇒ a − Δ a = k 2 λ D x M
⇒ 2 a = ( k 1 + k 2 ) . λ D a
⇒ 2 k = k 1 + k 2 .

Chọn đáp án C
Ta có: x A = k a λ D = k 1 a + Δ a λ D = k 2 a − 2 Δ a λ D .
Nên: k a = k 1 a + Δ a = k 2 a − 2 Δ a .
Áp dụng tính chất dãy tỷ số bằng nhau ta có: i T = λ D a = 15 λ 1 . D a = 15.0 , 4.10 − 6 .1 2.10 − 3 = 3.10 − 3 m
Vậy: 2 k 1 + k 2 = 3k.

Phương pháp: sử dụng công thức vân sáng
Cách giải:
Tại M là vân sáng bậc 9, bậc k, bậc 2 k nên có:
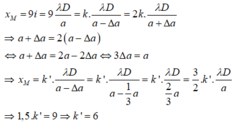
Đáp án B

Chọn A
Khi giảm đi 1 lượng Δa thì tại M là vân bậc k tức là:
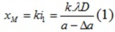
Khi tăng thêm 1 lượng Δa thì tại M là vân bậc k tức là:
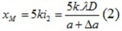
Từ (1) và (2) => a = 3Δa/2
=> Nếu tăng thêm khoảng cách S1S2 thêm 3Δa thì khoảng vân mới là:
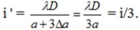
Lại có ban đầu M là vân sáng bậc 3 => xM = 3i => xM = 9i'
=> Sau khi tăng khoảng cách S1S2 thêm 3Δa thì tại M là vân sáng bậc 9

Chọn C
Khi giảm đi 1 lượng Δa thì tại M là vân bậc k tức là:
![]()
Khi tăng thêm 1 lượng Δa thì tại M là vân bậc k tức là:
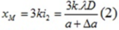
Từ (1) và (2) => a = 2Δa
=> Nếu tăng thêm khoảng cách S1S2 thêm 2Δa thì khoảng vân mới là:
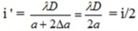
Lại có ban đầu M là vân sáng bậc 4 => xM = 4i => xM = 8i'
=> Sau khi tăng khoảng cách S1S2 thêm 2Δa thì tại M là vân sáng bậc 8
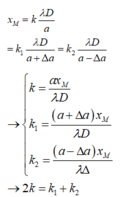



Đáp án A
+ Tại M là vị trí của vân sáng bậc k: x M = k D λ a → a = k D λ x M
Thay đổi a một lượng ∆a, ta có