Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
+ Vị trí vân sáng cùng màu vân trung tâm là: k 1 λ 1 = k 2 λ 2 = k 3 λ 3 Û 5 k 1 = 6 k 2 và 4 = 5 k 3
® 10 k 1 = 12 k 2 =15 k 3
+ Vị trí vân sáng giống vân trung tâm ứng với: k 1 = 0, 6, 12, …; k 2 = 0, 5, 10, …; k 3 = 0, 4, 8, …
+ Số vân váng trong miền MN của λ 1 là x = 6 - 1 = 5
+ Số vân váng trong miền MN của λ 2 là y = 5 - 1 = 4
+ Số vân váng trong miền MN của λ 3 là z = 4 - 1 = 3
® y + z = 7

Áp dụng công thức
λD
i = ▬▬
a
=> i1 = 0,64 mm
=> i2 = 0,54 mm
=> i3 = 0,48 mm
L = 40 mm
L/2 = 20 mm
Số vân i1 => 20 / 0,64 = 31,25 --> Có 31 vân sáng
Với màn bên kia cũng là 31
=> 62 vân
Số vân trùng
i1 k2 0.64 32
▬ = ▬▬ = ▬▬▬ = ▬▬
i2 k1 0,54 27
i1 k3 0.64 4 8 12 16 20 24 28 32 36 40
▬ = ▬▬ = ▬▬▬ = ▬ = ▬ = ▬▬ = ▬▬ = ▬▬ = ▬▬ = ▬▬ = ▬▬ = ▬▬ = ▬▬
i3 k1 0,48 3 6 9 12 15 18 21 24 27 30
Tổng số vân trùng 1 bên là 10 => Còn 62 - 10.2 = 42 vân
Đáp số 42 vân

Đáp án B
+ Vị trí vân sáng trùng nhau nên:
![]()
+ Vì M, N, P liên tiếp là các vân sáng trùng vân trung tâm nên tương ứng với
![]()
+ Với ánh sáng λ 1 thì có 7 giá trị thỏa mãn.
+ Với ánh sáng λ 2 thì có 9 giá trị thỏa mãn.

Đáp án D
+ Vị trí vân sáng trùng nhau tương ứng là:
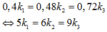
+ Vì M và N là 2 vị trí liên tiếp cho vạch sáng cùng màu vạch trung tâm nên tương ứng ta có:
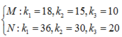
+ Vì không tính M và N nên
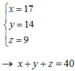




Đáp án C
Ta có: 0,4k1 = 0,48k2 = 0,6k3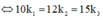
BCNN(10, 12, 15) = 60
→ Các cặp trùng nhau:
Nếu thực hiện lần lượt giao thoa với từng bức xạ, với λ1 không tính M, N thì có 23 vân sáng
Chứng tỏ tại N là vân trung tâm (0, 0, 0), tại M là vân trùng (24, 20, 16)
→ y = 20 – 1 = 19, z = 16 – 1 = 15