Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Ta có: k 1 k 2 = λ 2 λ 1 = 0 , 4 0 , 6 = 2 3 = 2 n 3 n ⇒ k 1 = 2 n
Vị trí vân sáng trùng: x s t = k 1 i 1 = k 2 i 2 ⇒ x s t = 2 n i 1
Số vân sáng trùng trong khoảng giữa 2 vân bậc 7 của λ 1 = λ thỏa điều kiện:
− 7 i 1 < x s t < 7 i 1 ⇔ − 7 i 1 < 2 n i 1 < 7 i 1 ⇔ − 3 , 5 < n < 3 , 5 ⇒

Đáp án D
Phương pháp: Công thức xác định vị trí vân tối x t = k + 1 2 λ D a
Cách giải: Ta có:
 Mà
Mà 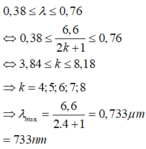




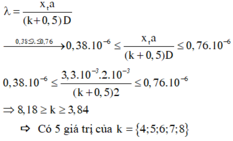


Áp dụng công thức
λD
i = ▬▬
a
=> i1 = 0,64 mm
=> i2 = 0,54 mm
=> i3 = 0,48 mm
L = 40 mm
L/2 = 20 mm
Số vân i1 => 20 / 0,64 = 31,25 --> Có 31 vân sáng
Với màn bên kia cũng là 31
=> 62 vân
Số vân trùng
i1 k2 0.64 32
▬ = ▬▬ = ▬▬▬ = ▬▬
i2 k1 0,54 27
i1 k3 0.64 4 8 12 16 20 24 28 32 36 40
▬ = ▬▬ = ▬▬▬ = ▬ = ▬ = ▬▬ = ▬▬ = ▬▬ = ▬▬ = ▬▬ = ▬▬ = ▬▬ = ▬▬
i3 k1 0,48 3 6 9 12 15 18 21 24 27 30
Tổng số vân trùng 1 bên là 10 => Còn 62 - 10.2 = 42 vân
Đáp số 42 vân
vậy vị trí ba vân trùng nhau thì sao?