Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khoảng vân: \(i=\dfrac{\lambda D}{a}=\dfrac{0,5\cdot10^{-6}\cdot1,5}{3\cdot10^{-3}}=2,5\cdot10^{-4}m=0,25mm\)
Điểm M cách vân trung tâm 1,25mm nên:
\(x=1,25mm=k\cdot i=k\cdot0,25\)
\(\Rightarrow k=5\Leftrightarrow\)M là vân sáng bậc 5.
Chọn A

Chọn B
tại vị trí cách vân trung tâm 3,6mm, ta thu được vân sáng bậc 3 tức là:
3i = 3,6mm => i = 1,2mm.
=> Vân tối thứ 3 cách vân trung tâm một khoảng: x = 2,5i = 3mm.

Khoảng vân: \(i=\dfrac{\lambda D}{a}=\dfrac{0,5\cdot10^{-6}\cdot2}{0,5\cdot10^{-3}}=2\cdot10^{-3}m=2mm\)
Tại điểm M cách vân trung tâm 7mm nên:
\(x=7mm=k\cdot i=k\cdot2\)
\(\Rightarrow k=3,5\Rightarrow\)M là vân tối thứ 4.
Chọn B.

Số vân sáng trong khoảng MN chính là số k thỏa mãn
\(x_M < x_s < x_N\)
=> \( 2 < k i < 4,5 \)
=> \(1,67 < k < 3,75.\)
Do \(k \in Z \) => \( k = 2,3.\)
Tương tự.
Số vân tối trong khoảng MN chính là số k thỏa mãn
\(x_M < x_t < x_N\)
=> \( 2 < (k+\frac{1}{2})i < 4,5\)
=> \( 1,167 < k < 3,25.\)
Do \(k \in Z \) => \(k = 2,3.\)
Vẫn chưa hiểu tại đoạn: k∈Z => k=2,3. Ai giải thích cho mình với ạ.

Chọn D
Ta có khoảng cách giữa một vân tối và một vân sáng liền kề là
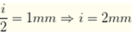
M và N ở hai phía so với vân trung tâm.
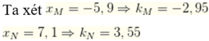
Vậy giữa M và N có 6 vân sáng
