Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
+ Khi sử dụng ánh sáng đơn sắc λ 1 và λ 2 , ta thấy giữa hai vân sáng gần nhau nhất cùng màu với vân trung tâm có 6 vân sáng ứng với λ 2 → Nếu ta xét vân đầu tiên trùng giữa hai hệ vân vân trung tâm thì vân thứ hai trùng nhau của hai hệ vân của bức xạ λ 2 ứng với k = 7.
→ Áp dụng điều kiện cho vân sáng trùng nhau của λ 1 và λ 2 → k 1 λ 1 = 7 λ 2 → λ 2 = k 1 . 0 , 56 7 = 0 , 08 k 1 .
+ Dựa vào khoảng giá trị của λ 2 là 0,65 μm < λ 2 < 0,75 μm → λ 2 = 0,72 μm.
+ Khi sử dụng ánh áng thì nghiệm gồm ba bức xạ đơn sắc, trong đó λ 3 = 2 3 λ 2 = 0 , 48 μm.
→ Áp dụng điều kiện trùng nhau của ba hệ vân k 1 λ 1 = k 2 λ 2 = k 3 λ 3 ↔ 7 k 1 = 9 λ 2 = 6 k 3
→ Tại vị trí trùng nhau của ba hệ vân sáng gần vân trung tâm nhất thì
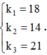
+ Điều kiện trùng nhau của vân sáng của hai bức xạ λ 1 và λ 2 là
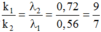
→ Giữa vân trung tâm và vân trùng màu gần vân trung tâm nhất có 1 vị trí trùng giữa vân sáng của λ 1 và λ 2 .
+ Điều kiện trùng nhau của vân sáng của hai bức xạ λ 3 và λ 2 là
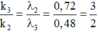
k 3 = 3, 6, 9, 12, 15, 18, 21
k 2 = 2, 4, 6, 8, 10, 12, 14
→ Giữa vân trung tâm và vân trùng màu gần vân trung tâm nhất có 6 vị trí trùng giữa vân sáng của λ 3 và λ 2 .
→ Giữa vân trung tâm và gân trùng màu gần nhất với vân trung tâm có 6 vân sáng đỏ

Đáp án A
+ Điều kiện để hai vân sáng trùng nhau λ d λ l = k l k d = 5 3 → giữa hai vân trùng màu với vân trung tâm có 2 vân đỏ và 4 vân lục

Đáp án C
+ Trên màn, trong khoảng giữa hai vân sáng gần nhau nhất và cùng màu với vân sáng trung tâm có 8 vân sáng lục nên vân sáng lục trùng nhau là vân thứ 9: k1=9
+ Điều kiện trùng nhau của hai bức xạ:
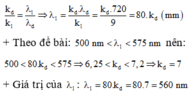




Đáp án B
Kể luôn 2 vân sáng trùng thì có 8 VS của λ2
=> có 7i2.
Gọi k là số khoảng vân của λ1 ;
Lúc đó ki1= 7i2 => kλ1= 7λ2
=> 0,67μm < λ2 = kλ1/7 < 0,74μm
=> 8,3 < k < 9,25 chọn k = 9
=> λ2 = 0,72μm
(Xét VS trùng gần VS TT nhất)
Khi 3 VS trùng nhau x1 = x2 = x3
Vị trí 3 VS trùng ứng với k1=9 , k2 = 7 , k3 = 12
Giữa hai Vân sáng trùng có 8 VS của λ1 ( k1 từ 1 đến 8)
6 VS của λ2 ( k2 từ 1 đến 6)
11 VS của λ3 ( k1 từ 1 đến 11)
Tổng số VS của 3 đơn sắc là 8+6+11= 25
Vì có 2 vị trí trùng của λ1 và λ3 ( với k1=3, k3=4 và k1=6, k3=8 )
nên số VS đơn sắc là 25 – 2= 23