Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp:
Sử dụng lí thuyết về giao thoa sóng ánh sáng
Khoảng vân: i = λD/a
Công thức tính số vân sáng trên bề rộng miền giao thoa L:
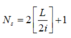
Cách giải:
Khoảng vân của bức xạ 1 là:
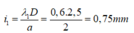
Số vân sáng của bức xạ 1 trên đoạn MN là:
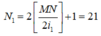
vân sáng
=> Số vân sáng của bức xạ 2 trên đoạn MN là N2 = N + NTr – N1 = 41 + 5 – 21 = 25 vân sáng
=> Khoảng vân của bức xạ 2 là i2 = MN/24 = 0,625mm
![]()
Chọn B

Chọn C
Trong bề rộng L=2,4 cm =24 mm có 33 vạch sáng có 5 vạch là kết quả trùng nhau của hai hệ vân nên ta có tổng số vân sáng thực sự do hai bức xạ tạo nên là 33+ 5 =38 vân.
Hai trong 5 vạch trùng nhau nằm ở ngoài cùng của trường giao thoa.
Như vậy ta có: 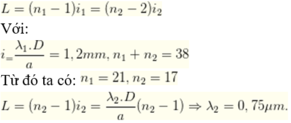

Chọn đáp án D
Ta có i = (λD)/a → i1 = 3 mm.
Bề rộng giao thoa L = k 1 i 1 = 24 mm → k 1 = 8. Vậy có 9 vân sáng ứng với ánh sáng có bước sóng λ 1 .
Có 17 vân sáng, 3 vân trùng nằm ở ngoài cùng → số vân sáng ứng với ánh sáng có bước sóng λ 2 là 11 vân. → k 2 = 10.
→ 24 = k 2 i 2 = 10i2 → i 2 = 2,4 mm.
→ λ 2 = a i 2 D = 0 , 2.10 − 3 .2 , 4.10 − 3 = 480 n m .

Ta có i = (λD)/a → i1 = 3 mm.
Bề rộng giao thoa L = k1i1 = 24 mm → k1 = 8. Vậy có 9 vân sáng ứng với ánh sáng có bước sóng λ1.
Có 17 vân sáng, 3 vân trùng nằm ở ngoài cùng → số vân sáng ứng với ánh sáng có bước sóng λ2 là 11 vân. → k2 = 10.
→ 24 = k2i2 = 10i2 → i2 = 2,4 mm.
![]()
Đáp án C

Đáp án A
Tổng số vân sáng mà hai hệ vân cho được là 33 + 5 = 38
+ Số vân sáng của bức xạ λ 1 cho trên màn
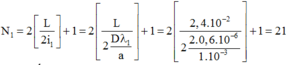
Vậy số vân sáng của bức xạ λ 2 trên màn sẽ là 38 – 21 = 17
→ Tại vị trí biên vân sáng bậc 10 của bức xạ λ 1 trùng với vân sáng bậc 8 của bức xạ λ 2
![]()



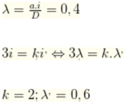
Đáp án B
+ Khoảng vân giao thoa của bức xạ λ 1
Số vị trí cho vân sáng của bức xạ λ 1 trên đoạn MN:
→ Vậy số vị trí cho vân sáng của bức xạ λ 2 trên đoạn MN là 41 + 5 – 11 = 25
Vì vị trí trùng nhau của hai hệ vân lặp lại có tính chu kì nên nêu ta xem M là vị trí vân trung tâm thì N sẽ là vị trí trùng nhau ứng với vân sáng bậc 20 của bức xạ λ 1 và vân sáng bậc 24 của bức xạ λ 2
Ta có: