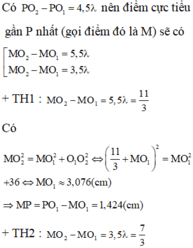Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
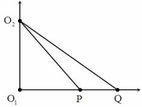
+ Vì Q dao động với biên độ cực đại nên: Q O 2 - Q O 1 = kl
+ Vì giữa P và Q còn có 1 cực đại và P dao động với biên độ cực tiểu nên:
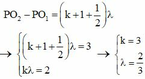
+ Điểm M gần P nhất nên sẽ ứng với k = 5
® M O 2 - M O 1
![]()
![]()
® OM » 3,1 cm
® MP » 1,4 cm

Có tan P O 2 Q = tan α - β = tan α - tan β 1 + tan α . tan β = 8 a - 4 ٫ 5 a 1 + 8 a . 4 ٫ 5 a = 3 ٫ 5 a + 36 a
Áp dụng BĐT Cauchy cho mẫu, ta tìm được
tan P O 2 Q ≤ 3 ٫ 5 12 ⇒ P O 2 Q m a x ⇔ a = 6 c m .
Q là cực đại, P là cực tiểu gần nguồn hơn và gần Q nhất nên ta có :
Q O 2 - Q O 1 = k λ P O 2 - P O 1 = k + 0 ٫ 5 λ ⇔ k λ = 2 k + 0 ٫ 5 λ = 3 ⇔ λ = 2 c m k = 1
Gọi M là cực đại gần P nhất. Vì Q là cực đại với k = 1 nên M là cực đại với k = 2.
⇒ M O 2 - M O 1 = 2 λ = 4 ⇒ M O 1 2 + 36 - M O 1 = 4 ⇔ M O 1 = 2 ٫ 5 c m
Suy ra PM = 4,5 – 2,5 = 2 (cm).


P O 2 - P O 1 = k + 0 ٫ 5 λ Q O 2 - Q O 1 = k λ ⇒ k + 0 ٫ 5 λ = 3 k λ = 2 ⇒ λ = 2 c m

Đáp án B
Đặt
![]()
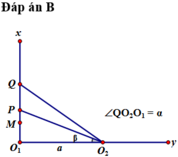
Theo hình vẽ ta có :
![]()
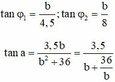
Theo bất đẳng thức cosi thì a=a max khi b = 6 cm
Suy ra :
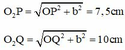
Tại Q là phần tử nước dao động với biên độ cực đại nên : ![]()
Tại P là phần tử nước không dao động nên P thuộc cực tiểu bậc k’
![]()
![]()
với k’ = k + 1 (do giữa P và Q không còn cực đại nào)
![]()
![]()
Q là cực đại ứng với k = 1 nên cực đại M gần P nhất ứng với k = 2
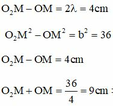
![]() hay OM = 2,5 cm
hay OM = 2,5 cm
Do đó : MP = 5,5 – 2,5 = 2 cm.

Đáp án A
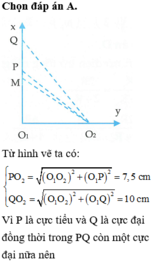
Từ hình vẽ ta có PO 2 = O 1 O 2 2 + O 1 P 2 = 7 , 5 cm QO 2 = O 1 O 2 2 + O 1 Q 2 = 10 cm
Vì P là cực tiểu và Q là cực đại đồng thời trong PQ còn một cực đại nữa nên PO 2 − PO 1 = 7 , 5 − 4 , 5 = k + 2 , 5 λ QO 2 − QO 1 = 10 − 8 = k − 1 λ ⇒ λ = 2 3 cm k = 4
P thuộc cực tiểu thứ 5 (k = 4) nên M là cực đại thuộc OP gần P nhất thì M phải thuộc cực đại bậc 5
Do đó MO 2 − MO 1 = 5 λ ⇒ OM 2 + O 1 O 2 2 − OM = 5 λ ⇒ OM = 3 , 73 cm
Vậy M cách P đoạn MP = OP − OM = 4 , 5 − 3 , 73 = 0 , 77 cm

Đáp án B
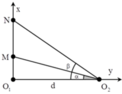
+ Ta có tan α = a d tan β = b d với d = O 1 O 2 = 18 c m .
tan M O 2 N ^ = tan β - α = tan β - tan α 1 + tan β tan α = a d - b d 1 + a d b d = d a - b d 2 + a b
+ Kết hợp a b = 324 ⇒ a = 324 b .
→ tan M O 2 N ^ = tan β - α = 1 36 b - 324 b = f b .
+ Ta có f ' b = 1 36 1 + 324 b 2 > 0 ∀ b trong 21 , 6 ; 24
→ M O 2 N ^ cực đại khi b=24cm, O 2 N = 30 c m O 2 M = 22 , 5 c m
+ M và N là hai cực đại ứng với bậc k và k+2, ta có:
O 2 M - a = k + 2 λ O 2 N - b = k λ ⇔ 22 , 5 - 13 , 5 = k + 2 λ 30 - 24 = k λ ⇒ λ = 1 , 5 c m .
Số cực đại giao thoa trên O 1 O 2 :
- O 1 O 2 λ ≤ k ≤ O 1 O 2 λ ⇔ - 18 1 , 5 ≤ k ≤ 18 1 , 5 ⇔ - 12 ≤ k ≤ 12 -> Có 25 điểm

Đáp án B
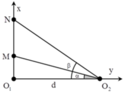
+ Ta có tan α = a d tan β = b d với d = O 1 O 2 = 18 c m .
tan M O 2 N ^ = tan β - α = tan β - tan α 1 + tan β tan α = a d - b d 1 + a d b d = d a - b d 2 + a b
Kết hợp a b = 324 ⇒ a = 324 b .
→ tan M O 2 N ^ = tan β - α = 1 36 b - 324 b = f b .
+ Ta có f ' b = 1 36 1 + 324 b 2 > 0 ∀ b trong 21 , 6 ; 24
→ M O 2 N ^ cực đại khi b=24cm. → a = 13 , 5 c m , O 2 N = 30 c m , O 2 M = 22 , 5 c m
+ M và N là hai cực đại ứng với bậc k và k+2, ta có:
O 2 M - a = k + 2 λ O 2 N - b = k λ ⇔ 22 , 5 - 13 , 5 = k + 2 λ 30 - 24 = k λ ⇒ λ = 1 , 5 c m .
Số cực đại giao thoa trên O 1 O 2 :
- O 1 O 2 λ ≤ k ≤ O 1 O 2 λ ⇔ - 18 1 , 5 ≤ k ≤ 18 1 , 5 ⇔ - 12 ≤ k ≤ 12
-> có 25 điểm