Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
Thời gian dùng MXH | 30 | 45 | 60 | 75 | 80 | 90 | 120 |
Số HS nam | 1 | 1 | 4 | 2 | 1 | 2 | 3 |
Thời gian dùng MXH | 30 | 45 | 60 | 75 | 80 | 90 | 120 |
Số HS nữ | 3 | 2 | 3 | 1 | 2 | 2 | 2 |
| Số trung bình | \({Q_1}\) | Trung vị (\({Q_2}\)) | \({Q_3}\) |
Nữ | 67,1875 | 45 | 60 | 85 |
Nam | 77,5 | 60 | 75 | 90 |
+) số trung bình: các HS nam sử dụng mạng xã hội nhiều hơn so với HS nữ
+) trung vị: các HS nam sử dụng mạng xã hội nhiều hơn so với HS nữ
+) tứ phân vị: thời gian sử dụng phân bố đồng đều ở cả năm và nữ.
b)
| Khoảng biến thiên | Khoảng tứ phân vị | Độ lệch chuẩn |
Nữ | 90 | 40 | 27,78 |
Nam | 90 | 30 | 27,1 |
Theo kết quả trên: Thời gian sử dụng mạng xã hội của các học sinh nữ có nhiều biến động hơn (một chút) so với các học sinh nam.

Bảng phân bố tần số
Thời gian hoàn thành một sản phẩm ở một nhóm công nhân
| Thời gian (phút) | 42 | 44 | 45 | 48 | 50 | 54 | cộng |
| Tần số | 4 | 5 | 20 | 10 | 8 | 3 | 50 |
Bảng phân bố tần suất
Thời gian hoàn thành một sản phẩm ở một nhóm công nhân
| Thời gian (phút) | 42 | 44 | 45 | 48 | 20 | 54 | Cộng |
| Tần suất (%) | 8 | 10 | 40 | 20 | 16 | 6 | 100% |

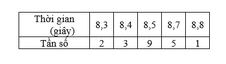
Ta có: số trung bình của bảng số liệu là
x - = ( 8 , 3 . 2 + 8 , 4 . 3 + 8 , 5 . 9 + 8 , 7 . 5 + 8 , 8 . 1 ) 20 = 8 , 53
Chọn D.

Số bạn trong lớp là \(n = 5 + 7 + 10 + 8 + 6 = 36\)
Thời gian chạy trung bình cự li 100 m của các bạn trong lớp là
\(\bar X = \frac{{5.12 + 7.13 + 10.14 + 8.15 + 6.16}}{{36}}\)
Chú ý
Bài toán này cho dưới dạng bảng tần số nên cần tính theo công thức trên.

Số giây trung bình để chạy 100 mét của các bạn học sinh ở nhóm A là:
\(\frac{{12,2 + 13,5 + 12,7 + 13,1 + 12,5 + 12,9 + 13,2 + 12,8}}{8} \approx 12,65\)
Số giây trung bình để chạy 100 mét của các bạn học sinh ở nhóm B là:
\(\frac{{12,1 + 13,4 + 13,2 + 12,9 + 13,7}}{5} = 13,06\)
Vậy nhóm A có thành tích chạy tốt hơn.

Trong mẫu số liệu trên; các giá trị 15; 13; 16 đều xuất hiện nhiều nhất – là 3 lần.
Do đó; mốt của mẫu số liệu trên là : 15; 13; 16
Chọn D

a)
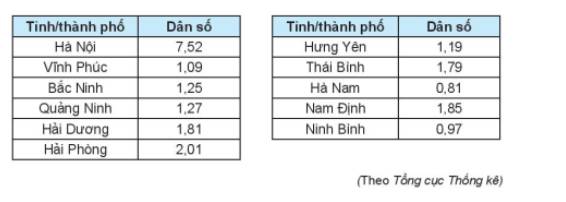
Sắp xếp lại:
0,81 | 0,97 | 1,09 | 1,19 | 1,25 | 1,27 | 1,79 | 1,81 | 1,85 | 2,01 | 7,52 |
Số trung bình Có 11 tỉnh thành nên n=11.
\(\begin{array}{l}\overline X = \frac{{7,52 + ... + 1,19 + ... + 0,97}}{{11}}\\ = 1,96\end{array}\)
Trung vị: 1,27
b) Ta thấy 7,52 lệch hẳn so với giá trị trung bình nên đây là giá trị bất thường của mẫu số liệu
=> Số trung bình và trung vị lại có sự sai khác nhiều
c) Nên sử dụng trung vị để đại diện cho dân số của các tỉnh thuộc Đồng bằng Bắc Bộ.






a)
+) Số trung bình: \(\overline x = \frac{{1.5 + 3.6 + 5.7 + 2.8 + 1.35}}{{1 + 3 + 5 + 2 + 1}} = 9,08\)
+) Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm, \(5,6,6,6,7,7,7,7,7,8,8,35\)
Bước 2: Vì \(n = 12\), là số chẵn nên \({Q_2} = \frac{1}{2}(7 + 7) = 7\)
\({Q_1}\) là trung vị của nửa số liệu: \(5,6,6,6,7,7\) Do đó \({Q_1} = \frac{1}{2}(6 + 6) = 6\)
\({Q_3}\) là trung vị của nửa số liệu \(7,7,7,8,8,35\) Do đó \({Q_3} = \frac{1}{2}(7 + 8) = 7,5\)
+) Mốt \({M_o} = 7\)
b)
+) Nếu so sánh số trung bình: 9,08 > 7 do đó thời gian thi nói chung của các thí sinh trong năm nay là lớn hơn so với năm trước.
+) Nếu so sánh trung vị: Trung vị của hai năm đều bằng 7 do đó thời gian thi nói chung của các thí sinh trong hai năm là như nhau.
Do có 1 thí sinh có thời gian thi lớn hơn hẳn so với các thí sinh khác => nên so sánh theo trung vị.