Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
a) Xét tam giác AOD có M là trung điểm của AO (gt) Q là trung điểm của OD (gt)
\(\Rightarrow MQ//AD,MQ=\frac{1}{2}AD\left(tc\right)\left(1\right)\)
CMTT \(MN//AB,MN=\frac{1}{2}AB\left(2\right)\)
\(NP=\frac{1}{2}BC\left(3\right)\)
\(PQ=\frac{1}{2}DC\left(4\right)\)
Mà AB=BC=CD=DA (tc) (5)
Từ (1) ,(2) ,(3),(4) và (5)\(\Rightarrow MN=NP=PQ=MQ\)
Xét tứ giác MNPQ có \(MN=NP=PQ=MQ\left(gt\right)\)
\(\Rightarrow MNPQ\)là hình thoi ( dhnb) (6)
Ta có: \(\hept{\begin{cases}MQ//AD\left(cmt\right)\\MN//AB\left(cmt\right)\end{cases}}\)mà \(AD\perp AB\)
\(\Rightarrow MQ\perp MN\)
\(\Rightarrow\widehat{QMN}=90^0\)(7)
Từ (6) và (7) \(\Rightarrow MNPQ\)là hình vuông (dhnb )
b) Ta có\(MQ=\frac{1}{2}AD\left(cmt\right)\)
mà \(AD=16\left(cm\right)\)
\(\Rightarrow MQ=8\left(cm\right)\)
\(\Rightarrow S_{MNPQ}=8^2=64\left(cm^2\right)\)
\(\Rightarrow S_{ABCD}=16^2=256\left(cm^2\right)\)
Vậy diện tích phần trong của hình vuông ABCD nằm ngoài tứ giác MNPQ =\(256-64=192\left(cm^2\right)\)
Kẻ \(BH\perp AD,CK\perp AD\)
\(\Rightarrow BH//CK\)
Ta có: \(\hept{\begin{cases}BH//CK\\BC//HK\end{cases}\Rightarrow BH=CK}\)( tc cặp đoạn chắn )
Xét tam giác ABD và tam giác ACD có:
2 đường cao BH,CK = nhau , đáy AD chung
\(\Rightarrow S_{ABD}=S_{ACD}\)
\(\Leftrightarrow S_{OAB}+S_{AOD}=S_{AOD}+S_{OCD}\)
\(\Leftrightarrow S_{OAB}=S_{OCD}\left(đpcm\right)\)
PS: có 1 tính chất học ở kì I lớp 8 á nhưng mình không biết cách giải thích sao nữa nên mình dùng cặp đoạn chắn

tgiác ABC có MN là đường trung bình => MN // AC và MN = AC/2
tgiác DAC có PQ là đường trung bình => PQ // AC và PQ = AC/2
vậy: MN // PQ và MN = PQ => MNPQ là hình bình hành
mặt khác xét tương tự cho hai tgiác ABD và CBD ta cũng có:
NP // BD và NP = BD/2
do giả thiết AC_|_BD => AC_|_NP mà MN // AC => MN_|_NP
tóm lại MNPQ là hình chữ nhật (hbh có một góc vuông)
b) MNPQ là hình vuông <=> MN = NP <=> AC/2 = BD/2 <=> AC = BD
vậy điều kiện là: tứ giác ABCD có hai đường chéo vuông góc và bằng nhau
c, Vỳ Mn là đườq trung bình của tam giác ABC nên MN= \(\frac{1}{2}\) AC= 3cm
QM là đường trung bình của tam giác ABD nên QM = \(\frac{1}{2}\) BD = 4cm
Mà MNPQ là hình chữ nhật nên diện tích ABCD = ( MN+PQ).2= (3.4):2 = 6cm
Bạn ơi lẽ ra chỗ diện tích hcn là phải bằng = 3 . 4 = 12cm chứ nhỉ bạn

a) xét tam giác ABC có:
AM=BM;BE=EC => ME là đường trung bình của tam giác ABC => ME=\(\frac{AC}{2}\)(1)
CMTT ta được : GN=\(\frac{AC}{2}\)(2)
\(GM=\frac{BD}{2}\)(3)
\(NE=\frac{BD}{2}\)(4)
Mà ABCD là hình thang cân nên AC=BD (5)
Từ (1),(2),(3),(4),(5) ta có : GM=ME=EN=NG \(\Rightarrow\)MENG là hình thoi.
b) do ABCD là hình thang cân nên chiều cao của hình thang ABCD là độ dài đường chéo MN trong hình thoi MENG.
độ dài đường cao của hình thang ABCD là:
800x2:(30+50)=20 (cm)
\(\Rightarrow\)MN=20 cm
Xét hình thang cân ABCD có:
AG=GD;BE=EC\(\Rightarrow\) GE là đường trung bình của hình thang cân ABCD
\(\Rightarrow\)\(GE=\frac{AB+DC}{2}\)
\(\Leftrightarrow\)\(GE=\frac{30+50}{2}=40\)(cm)
\(\Rightarrow\)DIện tích hình thoi MENG là: \(\frac{GE\times MN}{2}=\frac{20\times40}{2}=400\)\(\left(cm^2\right)\)
a) Ta có : ME // BD và \(ME=\frac{1}{2}BD\)
GN // BD và \(GN=\frac{1}{2}BD\Rightarrow ME//GN\)và \(ME=GN=\frac{1}{2}BD\)
Vậy MENG là hình bình hành
Tương tự , ta có : EN // MG và
\(EN=MG=\frac{1}{2}AC\)
Mặt khác ta lại có : BD = AC ( 2 đường chéo hình thang cân )
=> ME = GN = EN = MG , từ đó MENG là hình thoi
b) MN là đường trung bình của hình thang , nên :
\(MN=\frac{AB+CD}{2}=\frac{30+50}{2}=40\left(m\right)\)
EG là đường cao của hình thang nên MN . EG = 800 , suy ra :
\(EG=\frac{800}{40}=20\left(m\right)\)
DIện tích bồn hoa hình thoi là : \(\frac{1}{2}MN.EG=\frac{1}{2}.40.20=400\left(m^2\right)\)
a) ta có OM=OP và ON=OQ
=> MP=NQ và vuông góc tại O
Mà MP và NQ là đường chéo của MNPQ
=> MNPQ là hình vuông
AC= BD là cạnh huyền của vuông ABC và CDA mà
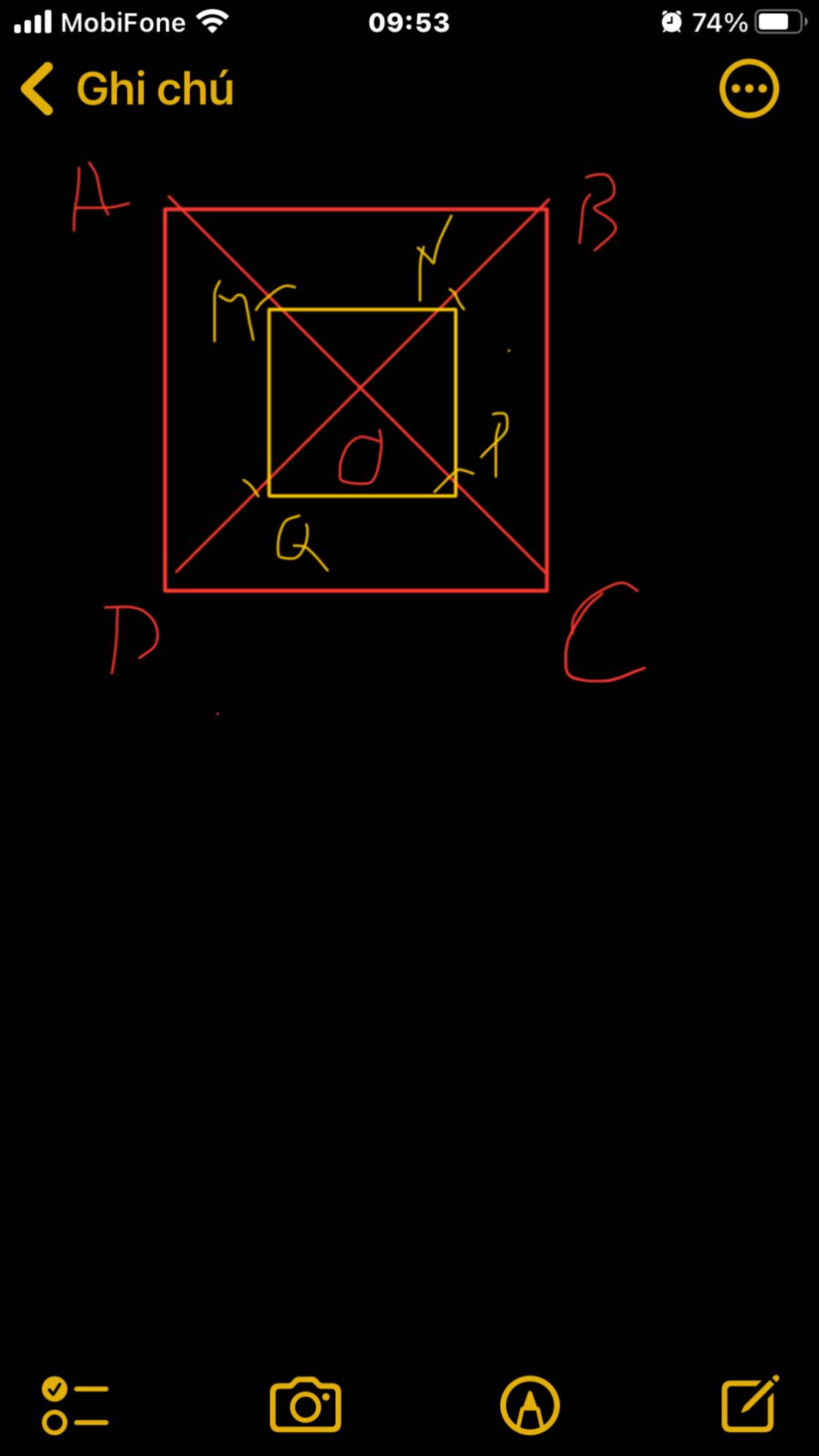
=> AC mũ 2 = 16mũ2 +16 mũ2. (bạn tự tính AC và BD nhé)
Tương tự MP= NQ =1/2AC
tính được MP và NQ thì sẽ tính được diện tích của MNQ và NPQ
Mà MNPQ = MNQ+NPQ