Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

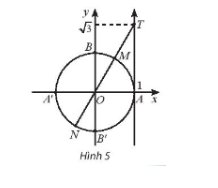
Những điểm biểu diễn góc x trên đường tròn lượng giác có \(tanx = \sqrt 3 \) là M và N.
Điểm M là điểm biểu diễn các góc lượng giác có số đo \(\frac{\pi }{3} + k2\pi ,k \in \mathbb{Z}\).
Điểm N là điểm biểu diễn các góc lượng giác có số đo \( - \frac{{2\pi }}{3} + k\pi ,k \in \mathbb{Z}\).

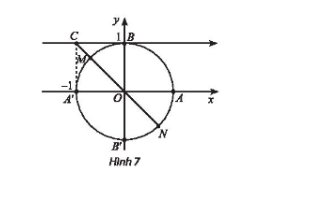
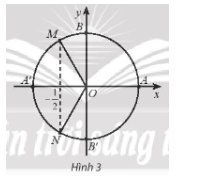
Điểm biểu diễn góc lượng giác x có \(cosx = \frac{{ - 1}}{2}\) là M và N.
Số đo góc lượng giác có điểm biểu diễn M là: \(\frac{{2\pi }}{3} + k2\pi ,k \in \mathbb{Z}\).
Số đo góc lượng giác có điểm biểu diễn N là: \(\frac{{4\pi }}{3} + k2\pi ,k \in \mathbb{Z}\).

a, Với mọi \(x\in R\), ta có: \(-1\le sin\left(x\right)\le1\)
Do đó, không có giá trị nào của x để \(sin\left(x\right)=1,5\)
b, Những điểm biểu diễn góc lượng giác có \(sin\left(x\right)=0,5\) là M và N.
Điểm M biểu diễn cho các góc lượng giác có số đo là \(\dfrac{\pi}{6}+k2\pi,k\in Z\)
Điểm N biểu diễn cho các góc lượng giác có số đo là \(\dfrac{5\pi}{6}+k2\pi,k\in Z\)

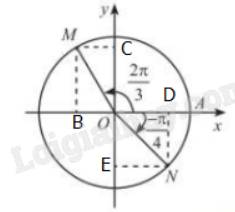
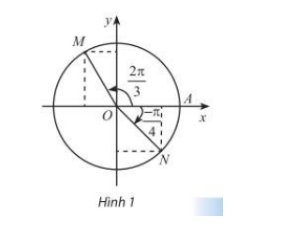
Gọi B, C lần lượt là hình chiếu của M lên Ox, Oy; D, E lần lượt là hình chiếu của N lên Ox, Oy
Ta có: OM = ON = 1
\(\widehat{MOC}=\dfrac{2\pi}{3}-\dfrac{\pi}{2}=\dfrac{\pi}{6}\\ \Rightarrow\left\{{}\begin{matrix}sin\widehat{MOC}=\dfrac{1}{2}\Rightarrow MC=\dfrac{1}{2}\\cos\widehat{MOC}=\dfrac{\sqrt{3}}{2}\Rightarrow MB=\dfrac{\sqrt{3}}{2}\end{matrix}\right.\)
Do điểm M có hoành độ nằm bên trái trục Ox nên tọa độ của điểm M là \(M\left(-\dfrac{1}{2};\dfrac{\sqrt{3}}{2}\right)\)
\(\widehat{NOD}=-\dfrac{\pi}{4}\\ \Rightarrow\left\{{}\begin{matrix}sin\widehat{NOD}=-\dfrac{\sqrt{2}}{2}\Rightarrow ND=-\dfrac{\sqrt{2}}{2}\\cos\widehat{NOD}=\dfrac{\sqrt{2}}{2}\Rightarrow NE=\dfrac{\sqrt{2}}{2}\end{matrix}\right.\)
Vậy tọa độ điểm N là \(N\left(\dfrac{\sqrt{2}}{2};-\dfrac{\sqrt{2}}{2}\right)\)

Tham khảo:
a) 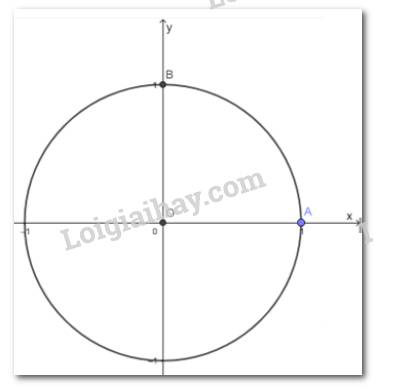
Góc lượng giác \(\left( {OA;OB} \right) = 90^\circ = \frac{\pi }{2}\)
b)
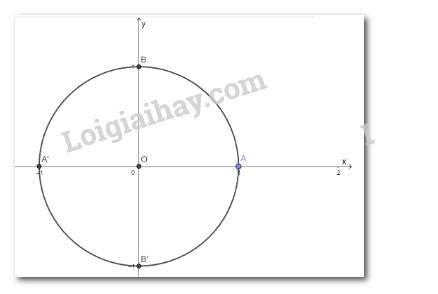

Chọn A
Phân tích.
- Ta thấy A thuộc đường phân giác trong góc A:x-3y+5=0 , giờ chỉ cần viết được phương trình AC là tìm được A.
- Trên AC đã có một điểm N, cần tìm thêm một điểm nữa. Chú ý khi lấy M’ đối xứng với M qua phân giác trong ta có M’ thuộc cạnh AC.
- Tìm M’ viết được phương trình AC từ đó suy ra A. Có A, M viết được phương trình AB.
- Gọi B, C và tham số hóa dựa vào B thuộc AB, C thuộc AC. Áp dụng công thức trọng tâm sẽ tìm ra được tọa độ B, C.
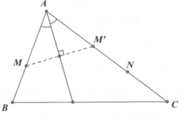




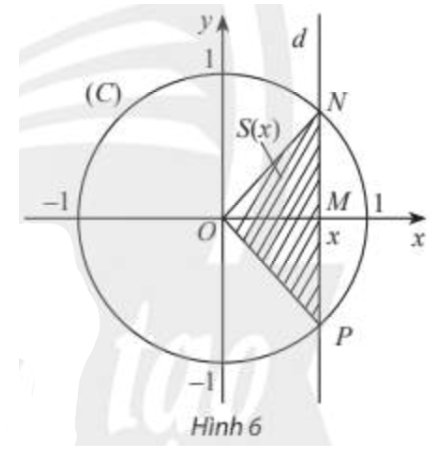
a) Ta có: \(\left( C \right):{x^2} + {y^2} = 1 \Leftrightarrow y = \pm \sqrt {1 - {x^2}} \).
Độ dài \(OM\) chính là giá trị tuyệt đối của hoành độ của điểm \(M\). Vậy \(OM = \left| x \right|\).
Độ dài \(MN\) chính là giá trị tuyệt đối của tung độ của điểm \(N\). Vậy \(MN = \left| {\sqrt {1 - {x^2}} } \right| = \sqrt {1 - {x^2}} \).
\(S\left( x \right) = {S_{ONP}} = \frac{1}{2}.NP.OM = MN.OM = \sqrt {1 - {x^2}} .\left| x \right|\).
b) Xét hàm số \(S\left( x \right) = \sqrt {1 - {x^2}} .\left| x \right| = \left\{ {\begin{array}{*{20}{c}}{x\sqrt {1 - {x^2}} }&{khi\,\,0 \le x \le 1}\\{ - x\sqrt {1 - {x^2}} }&{khi\,\, - 1 \le x < 0}\end{array}} \right.\).
ĐKXĐ: \(1 - {x^2} \ge 0 \Leftrightarrow - 1 \le x \le 1\)
Hàm số \(S\left( x \right)\) có tập xác định là \(\left[ { - 1;1} \right]\).
Vậy hàm số \(S\left( x \right)\) xác định trên các khoảng \(\left( { - 1;0} \right)\) và \(\left( {0;1} \right)\) nên liên tục trên các khoảng \(\left( { - 1;0} \right)\) và \(\left( {0;1} \right)\).
Ta có: \(S\left( 0 \right) = 0.\sqrt {1 - {0^2}} = 0\)
\(\mathop {\lim }\limits_{x \to {0^ + }} S\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \left( {x\sqrt {1 - {x^2}} } \right) = 0.\sqrt {1 - {0^2}} = 0\)
\(\mathop {\lim }\limits_{x \to {0^ - }} S\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} \left( { - x\sqrt {1 - {x^2}} } \right) = - 0.\sqrt {1 - {0^2}} = 0\)
Vì \(\mathop {\lim }\limits_{x \to {0^ + }} S\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} S\left( x \right) = 0\) nên \(\mathop {\lim }\limits_{x \to 0} S\left( x \right) = 0 = S\left( 0 \right)\)
Vậy hàm số \(S\left( x \right)\) liên tục tại điểm \({x_0} = 0\). Vậy hàm số \(S\left( x \right)\) liên tục trên \(\left( { - 1;1} \right)\).
c) \(\mathop {\lim }\limits_{x \to {1^ - }} S\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} \left( {x\sqrt {1 - {x^2}} } \right) = 1.\sqrt {1 - {1^2}} = 0\)
\(\mathop {\lim }\limits_{x \to - {1^ + }} S\left( x \right) = \mathop {\lim }\limits_{x \to - {1^ + }} \left( { - x\sqrt {1 - {x^2}} } \right) = - 1.\sqrt {1 - {{\left( { - 1} \right)}^2}} = 0\)

a:
i:
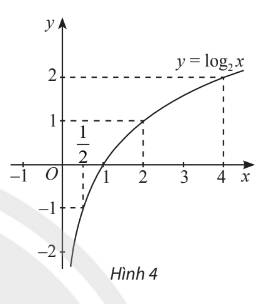
| x | 1/2 | 1 | 2 | 4 |
| y | -1 | 0 | 1 | 2 |
ii:
Hàm số liên tục và đồng biến trên \(\left(0;+\infty\right)\)
\(\lim\limits_{x\rightarrow+\infty}log_2x=+\infty;\lim\limits_{x\rightarrow0^+}log_2x=-\infty\)
Tập giá trị: R
b:
| x | 1/2 | 1 | 2 | 4 |
| y | 1 | 0 | -1 | -2 |
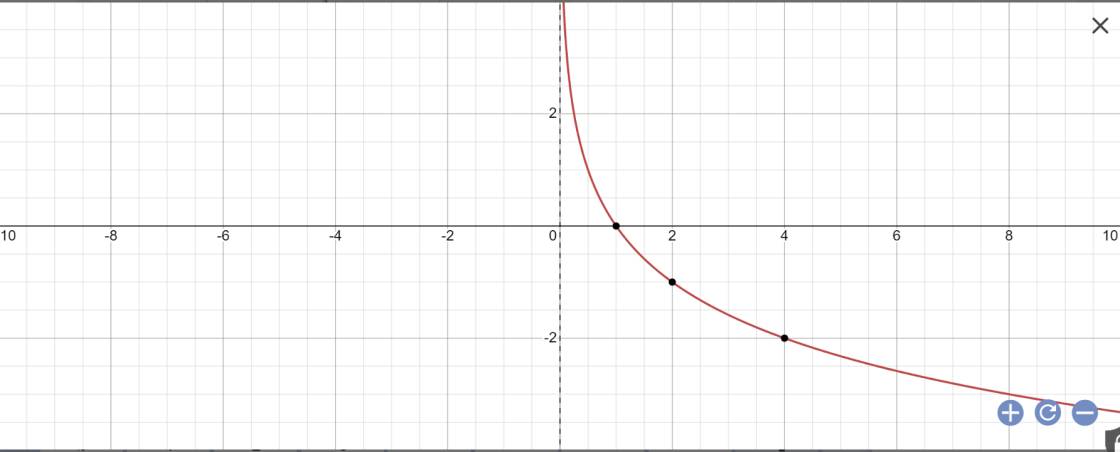
Hàm số liên tục và nghịch biến trên \(\left(0;+\infty\right)\)
\(\lim\limits_{x\rightarrow+\infty}log_{\dfrac{1}{2}}x=-\infty;\lim\limits_{x\rightarrow0^+}log_{\dfrac{1}{2}}x=+\infty\)
Tập giá trị: R

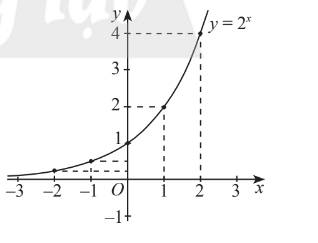
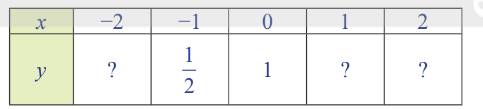
i:
| x | -2 | -1 | 0 | 1 | 2 |
| y | 1/4 | 1/2 | 1 | 2 | 4 |
ii:
Hàm số liên tục và đồng biến trên R
\(\lim\limits_{x\rightarrow+\infty}2^x=+\infty;\lim\limits_{x\rightarrow-\infty}2^x=0\)
Tập giá trị: \((0;+\infty)\)
b:
bảng giá trị:
| x | -2 | -1 | 0 | 1 | 2 |
| y | 4 | 2 | 1 | 1/2 | 1/4 |
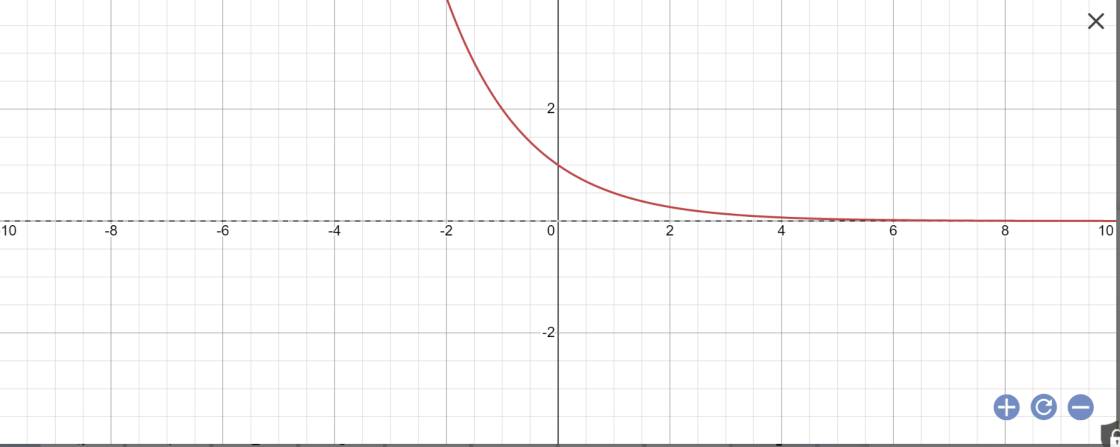
Hàm số liên tục và nghịch biến trên R
\(\lim\limits_{x\rightarrow+\infty}\left(\dfrac{1}{2}\right)^x=0;\lim\limits_{x\rightarrow-\infty}\left(\dfrac{1}{2}\right)^x=+\infty\)
Tập giá trị: (0;+\(\infty\))

Trên đường tròn lượng giác hai điểm M và N biểu diễn các góc lượng giác có số đo góc x thỏa mãn \(cotx = - 1\).
Điểm M biểu diễn các góc lượng giác có số đo góc \(\frac{{3\pi }}{4} + k2\pi ,k \in \mathbb{Z}\).
Điểm N biểu diễn các góc lượng giác có số đo góc \( - \frac{\pi }{4} + k2\pi ,k \in \mathbb{Z}\).