Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}m-3+n=-3\\-2m+n+6=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m+n=0\\-2m+n=-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3m=3\\m+n=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=1\\n=-1\end{matrix}\right.\)

Để tìm a và b, ta có các điều kiện sau:
Đường thẳng (d) có tung độ gốc là 1/3, tức là đường thẳng có dạng y = (1/3)x + b.Đường thẳng (d) cắt trục hoành tại điểm có hoành độ bằng 4, tức là khi x = 4, y = 0.Thay x = 4 và y = 0 vào phương trình đường thẳng, ta có:
0 = (1/3) * 4 + b 0 = 4/3 + b
Từ đó, ta có b = -4/3.
Vậy, phương trình đường thẳng (d) là: y = (1/3)x - 4/3.
(d) đi qua A(0;1/3) và B(4;0) nên ta có hệ phương trình:
0*a+b=1/3 và 4a+b=0
=>b=1/3 và 4a=-b=-1/3
=>a=-1/12 và b=1/3

\(\left\{{}\begin{matrix}a\cdot0+b=3\\-2a+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=3\\a=\dfrac{3}{2}\end{matrix}\right.\)

d: Để (d)//\(y=\dfrac{-2x-1}{5}=\dfrac{-2}{5}x-\dfrac{1}{5}\) thì
\(\left\{{}\begin{matrix}m-3=\dfrac{-2}{5}\\n\ne-\dfrac{1}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{13}{5}\\n\ne-\dfrac{1}{5}\end{matrix}\right.\)

a: Thay x=0 và y=2 vào (d), ta được:
\(0\left(m-1\right)+m=2\)
=>m+0=2
=>m=2
b: Thay x=-3 vào y=0 vào (d), ta được:
\(-3\left(m-1\right)+m=0\)
=>-3m+3+m=0
=>-2m+3=0
=>-2m=-3
=>\(m=\dfrac{3}{2}\)
c: Khi m=2 thì (d): \(y=\left(2-1\right)x+2=x+2\)
Khi m=3/2 thì (d): \(y=\left(\dfrac{3}{2}-1\right)x+\dfrac{3}{2}=\dfrac{1}{2}x+\dfrac{3}{2}\)
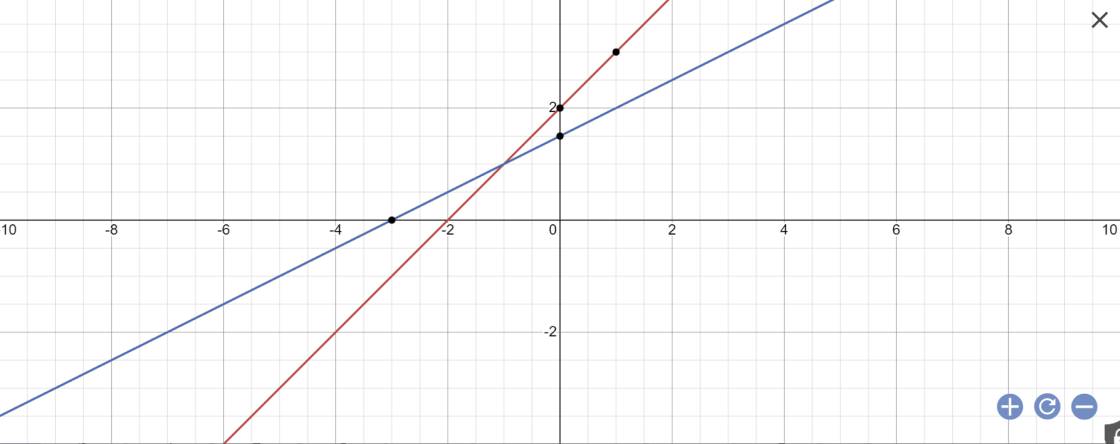
Tọa độ giao điểm của hai đường thẳng này là nghiệm của hệ phương trình sau:
\(\left\{{}\begin{matrix}x+2=\dfrac{1}{2}x+\dfrac{3}{2}\\y=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x-\dfrac{1}{2}x=\dfrac{3}{2}-2\\y=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{2}x=-\dfrac{1}{2}\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=-1+2=1\end{matrix}\right.\)
Tọa độ A(-1; - 1), B(1; 1), C(3; x)
Ta có
\(AB=\sqrt{2^2+2^2}=2\sqrt{2}\)
\(Bc=\sqrt{2^2+\left(x-1\right)^2}\)
\(CA=\sqrt{4^2+\left(x+1\right)^2}\)
Để tam giác ABC vuông tại A thì
AB2 + AC2 = BC2
<=> 8 + 16 + (x + 1)2 = 4 + (x - 1)2
<=> x = - 5
Vậy tọa độ C(3; - 5)
Điểm B ở đâu ra vậy bạn