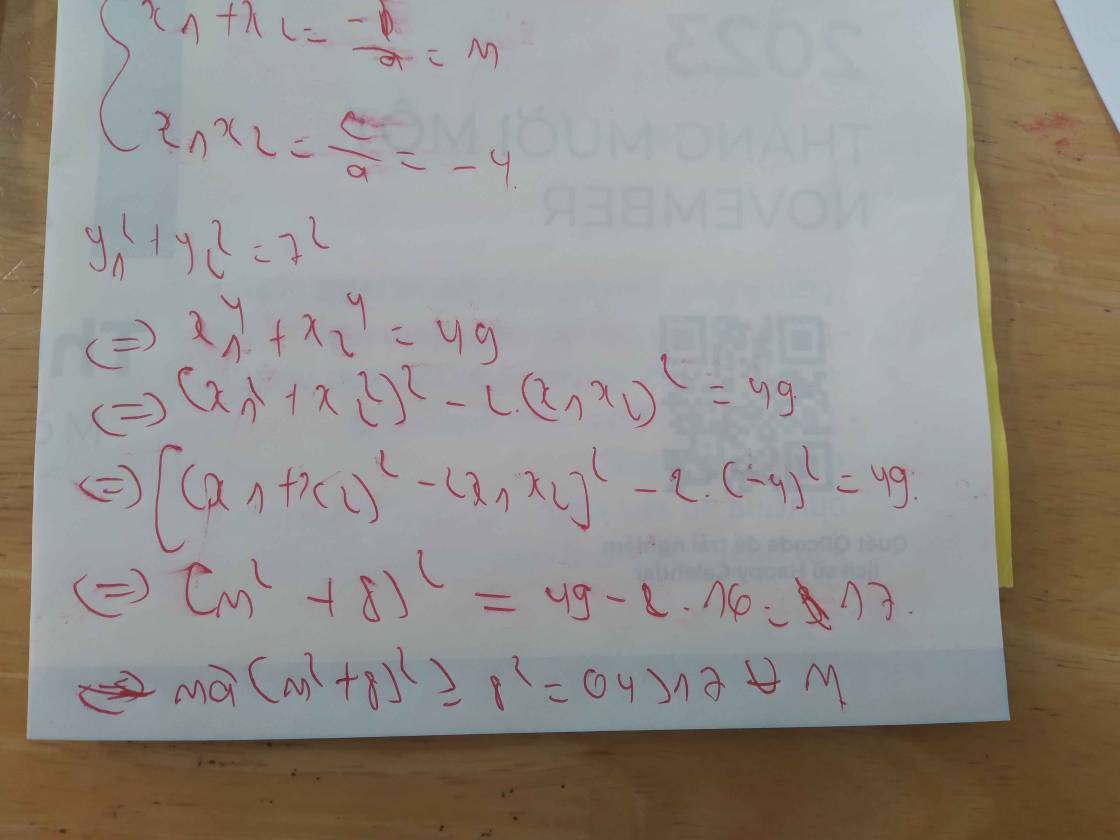Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: PTHĐGĐ là:
x^2-2x-|m|-1=0
a*c=-|m|-1<0
=>(d)luôn cắt (P) tại hai điểm phân biệt
b: Bạn bổ sung lại đề đi bạn

Phương trình hoành độ giao điểm là:
\(x^2-3x-m^2+1=0\)
\(\text{Δ}=\left(-3\right)^2-4\left(-m^2+1\right)=4m^2-4+9=4m^2+5>0\)
Do đó: (P) luôn cắt (d) tại hai điểm phân biệt

b: Phương trình hoành độ giao điểm là:
\(\dfrac{3}{2}x^2-mx-4=0\)
\(\Leftrightarrow3x^2-2mx-8=0\)
ac<0 nên (P) luôn cắt (d) tại hai điểm phân biệt
Theo đề, ta có: \(\left(x_1+x_2\right)^2-3x_1x_2=24\)
\(\Leftrightarrow m^2\cdot\dfrac{4}{9}-3\cdot\dfrac{-8}{3}=24\)
\(\Leftrightarrow m^2\cdot\dfrac{4}{9}=16\)
hay m=6 hoặc m=-6

pt hoành độ giao điểm của (p) và (d) là:
x2= 2(m+1)x -3m+2 ⇔ x2 -2(m+1)x +3m-2 =0(1)
a/ Thay m=3 vào pt (1) ta được: x2-8x+7=0(1')
pt (1') có: a+b+c=1-8+7=0
⇒x1=1; x2=\(\dfrac{c}{a}\)=7.
b/ pt (1) có:
Δ'= [-(m+1)]2- (3m-2)
= m2+2m+1-3m+2
=m2-m+3
=[(m-2.\(\dfrac{1}{2}\).m+\(\dfrac{1}{4}\))-\(\dfrac{1}{4}\)+3]
=(m-\(\dfrac{1}{2}\))2+\(\dfrac{11}{4}\)≥\(\dfrac{11}{4}\)>0 với mọi m
⇒pt(1)luôn có hai nghiệm phân biệt với mọi m
⇒(p) và (d) luôn cắt nhau tại hai điểm phân biệt với mọi m

- Xét phương trình hoành độ giao điểm : \(x^2=2mx-2m+3\)
\(\Leftrightarrow x^2-2mx+2m-3=0\left(I\right)\)
- Xét thấy để P và d cắt nhau tại hai điểm phân biệt khi PT ( I ) có hai nghiệm phân biệt .
\(\Leftrightarrow\Delta^,=b^{,2}-ac=m^2-\left(2m-3\right)>0\)
\(\Leftrightarrow m^2-2m+3>0\)
Mà \(m^2-2m+3=m^2-2m+1+2=\left(m+1\right)^2+2\ge2>0\forall m\in R\)
Vậy ... ĐPCM

b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}3x^2-2x-1=0\\y=3x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x^2-3x+x-1=0\\y=3x^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-1\right)\left(3x+1\right)=0\\y=3x^2\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(1;3\right);\left(-\dfrac{1}{3};\dfrac{1}{3}\right)\right\}\)