Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì AD ⊥ (ABC) nên AD ⊥ BC
Ngoài ra BC ⊥ AB nên ta có BC ⊥ (ABD)
Vì mặt phẳng (BCD) chứa BC mà BC ⊥ (ABD) nên ta suy ra mặt phẳng (BCD) vuông góc với mặt phẳng (ABD).
Hai mặt phẳng (BCD) và (ABD) vuông góc với nhau và có giao tuyến là BD. Đường thẳng AH thuộc mặt phẳng (ABD) và vuông góc với giao tuyến BD nên AH vuông góc với mặt phẳng (BCD).

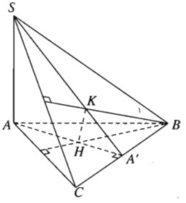
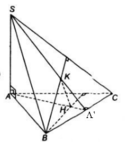
a) Gọi A’ là giao điểm của AH và BC. Ta cần chứng minh ba điểm S, K, A’ thẳng hàng.
Vì H là trực tâm của tam giác ABC nên AA′ ⊥ BC. Mặt khác theo giả thiết ta có: SA ⊥ (ABC), do đó SA ⊥ BC.
Từ đó ta suy ra BC ⊥ (SAA′) và BC ⊥ SA′. Vậy SA’ là đường cao của tam giác SBC nên SA’ là phải đi qua trực tâm K. Vậy ba đường thẳng AH, SK và BC đồng quy.
b) Vì K là trực tâm của tam giác SBC nên BK ⊥ SC (1)
Mặt khác ta có BH ⊥ AC vì H là trực tâm của tam giác ABC và BH ⊥ SA vì SA ⊥ (ABC).
Do đó BH ⊥ (ABC) nên BH ⊥ SC (2).
Từ (1) và (2) ta suy ra SC ⊥ (BHK). Vì mặt phẳng (SAC) chứa SC mà SC ⊥ (BHK) nên ta có (SAC) ⊥ (BHK).
c) Ta có
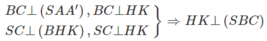
Mặt phẳng (BHK) chứa HK mà HK ⊥ (SBC) nên (BHK) ⊥ (SBC).