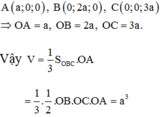Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
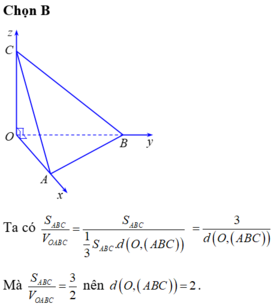
Vậy mặt phẳng (ABC) luôn tiếp xúc mặt cầu tâm O, bán kính R = 2.
Chọn D
Giả sử A (a; 0; 0), B (0; b; 0), C (0; 0; c) với a, b, c > 0
Khi đó mặt phẳng (P) có dạng 
.
Vì (P) đi qua M nên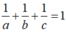 
Mặt khác OA = 2OB nên a = 2b nên 
Thể tích khối tứ diện OABC là: V= abc/6
Ta có:
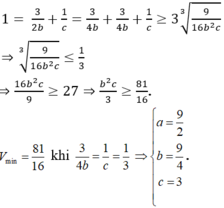
Đáp án B
Phương pháp:
Chứng minh khoảng cách từ O đến (ABC) không đổi.
Cách giải:
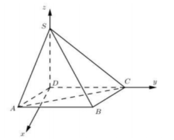
ta có
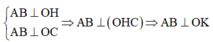
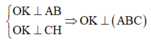
Ta sẽ chứng minh OK không đổi, khi đó mặt phẳng (ABC) luôn tiếp xúc với mặt cầu tâm O bán kính OK
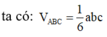
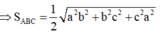
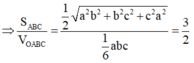
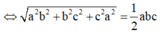
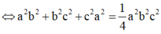
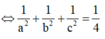
Xét tam giác vuông OCK có
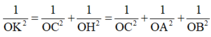
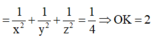
Vậy mặt phẳng (ABC) luôn tiếp xúc với mặt cầu tâm O bán kính 2
Đáp án A
Phương pháp giải:
Xét vị trí tương đối của mặt phẳng, gọi phương trình tổng quát của mặt phẳng và tính toán dựa vào điều kiện tiếp xúc
Lời giải:
Gọi phương trình mặt phẳng cần tìm là (P): ax+by+cz+d=0
suy ra mp(P)//BC hoặc đi qua trung điểm của BC.
Mà B C → = ( - 4 ; 0 ; 0 ) và mp vuông góc với mp (Oyz) => (P) //BC
Với (P) //BC => a = 0 => by+cz+d=0
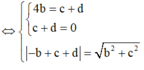
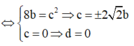
suy ra có ba mặt phẳng thỏa mãn
Đáp án B.
Lời giải sưu tầm :
Giả sử (P) tiếp xúc với (S1), (S2) lần lượt tại A,B
Gọi 
ta kiểm tra được J là trung điểm IM do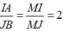 
suy ra M(2;1;9).
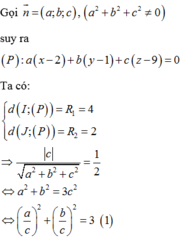
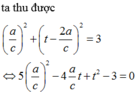
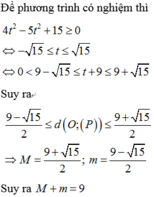
Chọn D
Gọi A (a;0;0), B (0;b;0), C (0;0;c), do A, B, C thuộc ba tia Ox, Oy, Oz nên a, b, c > 0.
