Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

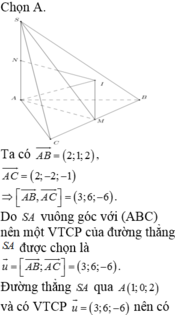
Chọn A.
Ta có
![]()
![]()
Do SA vuông góc với (ABC) nên một VTCP của đường thẳng SA được chọn là
![]()
Đường thẳng SA qua A(1;0;2) và có VTCP u → = ( 3 ; 6 ; - 6 ) nên có phương trình tham số là:
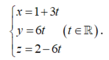
![]()
![]()
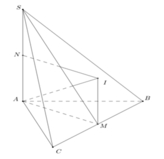
Gọi M là trung điểm BC khi đó M là tâm đường tròn ngoại tiếp tam giác ABC. Gọi d là đường thẳng qua M và song song với AS nên d ⊥ (ABC), suy ra d là trục đường tròn ngoại tiếp tam giác ABC.
Trong mặt phẳng (SAM) vẽ đường trung trực của SA cắt d tại I và cắt SA tại N.
Mặt phẳng (ABC) qua A và có một VTPT
![]()
nên có phương trình tổng quát là:
![]()
![]()
![]()
![]()
![]()
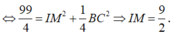
![]()
![]()
![]()
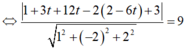
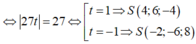
mà cao độ của S âm nên S(4;5;-4) thỏa yêu cầu bài toán.

Chọn B
Nhận thấy AB=AC=AD=BC=DB=DC= 2 nên ABCD là tứ diện đều cạnh 2 .
Theo giả thiết giao tuyến của mặt cầu tiếp xúc 6 cạnh của tứ diện với (ACD) là đường tròn nội tiếp tam giác ACD.
Gọi r là bán kính hình tròn nội tiếp tam giác ACD
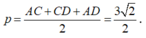
Khi đó diện tích tam giác đều ACD
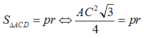
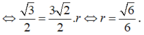
Diện tích thiết diện
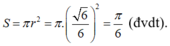
Cách 2:
Vì ABCD là tứ diện đều nên (ACD) cắt mặt cầu theo giao tuyến là đường tròn nội tiếp tam giác ACD . Suy ra tâm đường tròn này trùng với trọng tâm tam giác đều ACD và bán kính
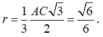
Diện tích thiết diện
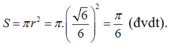

Đáp án C.
Vì OA = 1, OB = 2, OC = 3 và đôi một vuông góc
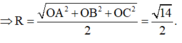

Chọn C
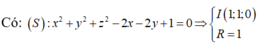
Gọi (P) là mặt phẳng thỏa mãn bài toán.
Ta có A (1; 0; 0) ∈ (S) => nếu tồn tại (P) thì (P) tiếp xúc với (S) tại A.
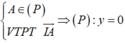
Ta thấy A (0; 0 ; 2) ∈ (P) duy nhất một mặt phẳng thỏa mãn bài toán.
Ghi chú: Bài toán này thường thường thì sẽ có hai mặt phẳng thỏa mãn, nhưng với số liệu của bài này thì chỉ có một mặt phẳng thỏa mãn bài toán.

Chọn B
Gọi tâm mặt cầu nội tiếp tứ diện OABC là I (x; y; z). Ta có phương trình (OBC): x - z = 0. Phương trình mặt phẳng (ABC): 5x + 3y + 4z - 15 = 0. Tâm I cách đều hai mặt phẳng (OBC) và (ABC) suy ra:
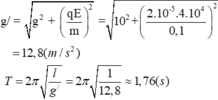
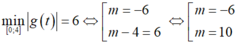
Nhận xét: hai điểm A và O nằm về cùng phía với (α) nên loại (α). Hai điểm A và O nằm về khác phía (β) nên nhận (β). Thấy ngay một vectơ pháp tuyến là (10; a; b) thì a = 3, b = -1. Vậy a + b = 2

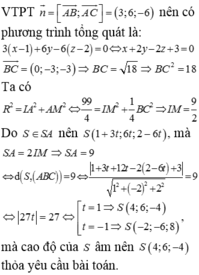

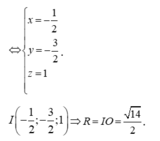

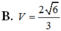

Chọn D
Tức là tứ diện SABC có các cạnh SA, SB, SC bằng nhau và đôi một vuông góc.
Vậy tứ diện SABC có tất cả ba mặt phẳng đối xứng đó là: