Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
- Qua điểm O có thể dựng vô số đường thẳng vuông góc với Δ, các đường thẳng đó cùng nằm trong một mặt phẳng vuông góc với Δ.

Đáp án B
- Phương pháp:
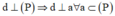
- Cách giải: Trong không gian cho đường thẳng Δ và điểm O. Qua O có vô số đường thẳng vuông góc Δ. Chúng nằm trong mặt phẳng qua O và vuông góc với Δ.

a) Sai
Sửa lại: "Đường thẳng Δ là đường thẳng vuông góc chung của hai đường thẳng chéo nhau a và b nếu Δ cắt cả a và b, đồng thời Δ ⊥ a và Δ ⊥ b"
b) Đúng
c) Đúng
d) Sai
Sửa lại: Đường thẳng đi qua M trên a và vuông góc với a, đồng thời cắt b tại N và vuông góc với b thì đó là đường vuông góc chung của a và b.
e) Sai.

Chọn C.
Đạo hàm: 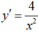
Đường thẳng Δ vuông góc với đường thẳng d: y = -x + 2 nên có hệ số góc bằng 1.
Ta có phương trình 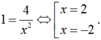
Tại M(2; 0). Phương trình tiếp tuyến là y = x – 2.
Tại N(-2; 4). Phương trình tiếp tuyến là y = x + 6.

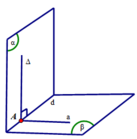
Δ nằm trong (α) và Δ vuông góc với d ⇒ Δ cắt d tại A
Từ A, vẽ đường thẳng a thuộc (β) và a ⊥ d
Khi đó góc giữa 2 mp (α) và (β) bằng góc giữa hai đường thẳng ∆ và a.
Vì (α) ⊥ (β) nên góc giữa Δ và a là 90° hay Δ ⊥ a
⇒ Δ ⊥ (d,a) hay Δ ⊥ (β)

tham khảo:
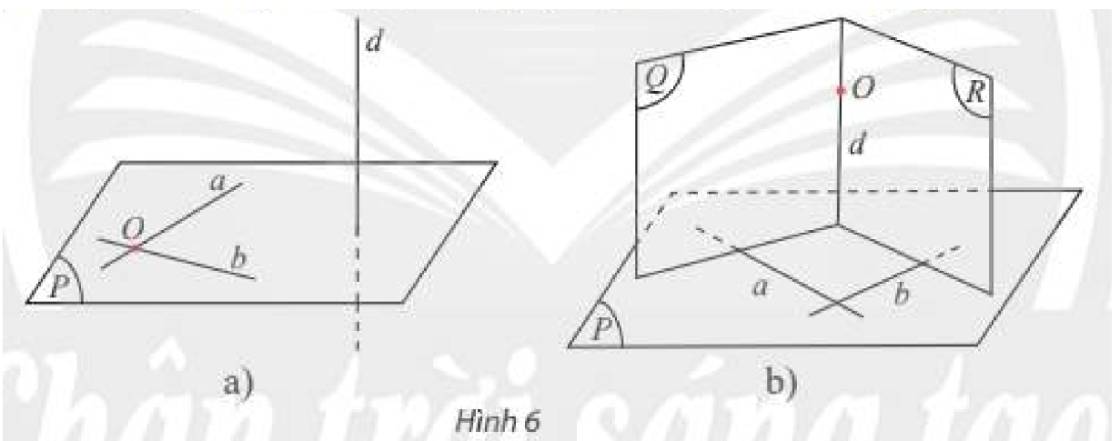
a) Vì đường thẳng d vuông góc hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) nên d⊥(P)
b) Vì a⊥(Q);d∈(Q) nên a⊥d
Vì b⊥(R),d∈(R) nên b⊥d
Vì đường thẳng d vuông góc hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) nên d⊥(P)
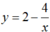
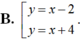
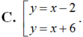
Chọn A