Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Có \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{2}{3}\)
- Có \(\frac{{B'C'}}{{BC}} = \frac{2}{3}\)
- Tam giác A'B'C' có đồng dạng với tam giác ABC và đồng dạng với tỉ số \(\frac{2}{3}\)

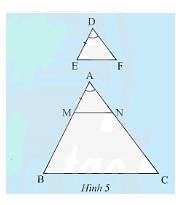
a) Vì \(MN//BC\left( {M \in AB,N \in AC} \right)\) nên \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\)(định lí Thales).
b) Vì \(AM = DE\) mà \(\frac{{DE}}{{AB}} = \frac{1}{3} \Rightarrow \frac{{AM}}{{AB}} = \frac{1}{3} \Rightarrow \frac{{AN}}{{AC}} = \frac{1}{3} \Rightarrow AN = \frac{1}{3}AC\).
Lại có \(DF = \frac{1}{3}AC\) nên \(AN = DF = \frac{1}{3}AC\).
c) Vì \(MN//BC \Rightarrow \Delta ABC\backsim\Delta AMN\) (định lí)(1)
d) Dự đoán hai tam giác \(DEF\) và \(ABC\) đồng dạng.

Xét tam giác ABC và tam giác ADB có
\(\widehat {ABC} = \widehat {A{\rm{D}}B}\) và \(\widehat A\) chung
=> ΔABC ∽ ΔADB (g.g)
=> \(\frac{{AB}}{{AD}} = \frac{{AC}}{{AB}}\)
=> \(A{B^2} = A{\rm{D}}.AC\)

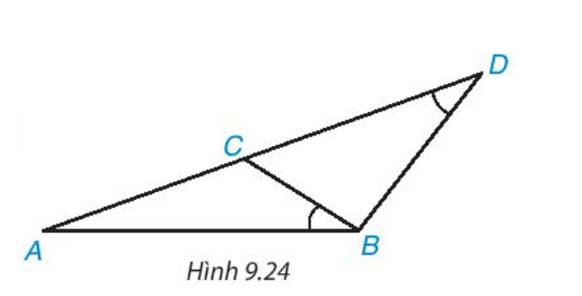
a) Xét tam giác \(ABD\) và tam giác \(ACB\) có:
\(\widehat {ABD} = \widehat {ACB}\) (giả thuyết)
\(\widehat A\) chung
Suy ra, \(\Delta ABD\backsim\Delta ACB\) (g.g)
b) Vì \(\Delta ABD\backsim\Delta ACB\)
Suy ra, \(\frac{{AB}}{{AC}} = \frac{{AD}}{{AB}}\) (các cặp cạnh tương ứng có cùng tỉ lệ).
Suy ra, \(A{B^2} = AC.AD = 9.4 = 36 \Rightarrow AB = \sqrt {36} = 6\)
Vậy \(AB = 6cm.\)

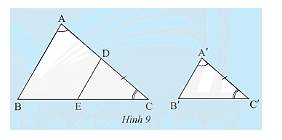
a) Vì \(ED//AB \Rightarrow \Delta DEC\backsim\Delta ABC\) (định lí)
b) Vì \(ED//AB \Rightarrow \widehat {CDE} = \widehat {CAB}\) (hai góc đồng vị)
Mà \(\widehat {CAB} = \widehat {A'}\). Do đó, \(\widehat {CDE} = \widehat {B'A'C'}\).
Xét tam giác \(A'B'C'\) và tam giác \(DEC\) ta có:
\(\widehat {B'A'C'} = \widehat {CDE}\) (chứng minh trên)
\(A'C' = CD\) (giải thuyết)
\(\widehat {C'} = \widehat C\) (giả thuyết)
Do đó, \(\Delta A'B'C' = \Delta DEC\) (g.c.g)
c) Vì tam giác \(\Delta A'B'C'\backsim\Delta DEC\) (tính chất)
Mà \(\Delta DEC\backsim\Delta ABC\) nên \(\Delta ABC\backsim\Delta A'B'C'\).

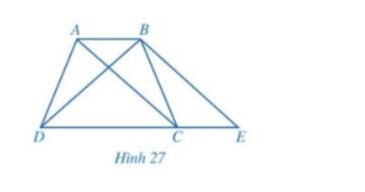
Do ABCD là hình thang nên AB//CD.
Kẻ BE//AC, \(E \in CD\) nên CE//AB.
\( \Rightarrow \widehat {BCE} = \widehat {ABC}\); \(\widehat {CBE} = \widehat {ACB}\) (hai góc so le trong).
a, Xét \(\Delta ABC\)và \(\Delta ECB\) có:
\(\widehat {BCE} = \widehat {ABC}\)
BC chung
\(\widehat {CBE} = \widehat {ACB}\) (do BC//AC )
\( \Rightarrow \Delta ABC = \Delta ECB\)(g.c.g)
b, BE = AC = BD
\( \Rightarrow \Delta BDE\)cân tại B
\( \Rightarrow \widehat {BDE} = \widehat {BED}\)
Do \(\Delta ABC = \Delta ECB\)
\( \Rightarrow \widehat {BEC} = \widehat {BAC}\) (2 góc tương ứng) hay \(\widehat {BED} = \widehat {BAC}(1)\)
Mà: \(\widehat {BAC} = \widehat {ACD}\) (do AB//CD) (2)
Từ (1), (2) suy ra: \(\widehat {BED} = \widehat {ACD}\)
c, Theo câu b:
\(\begin{array}{l}\widehat {BED} = \widehat {BDE}\\\widehat {ACD} = \widehat {BED}\end{array}\) suy ra: \(\widehat {ACD} = \widehat {BDE}\) hay \(\widehat {ACD} = \widehat {BDC}\)
Xét \(\Delta ACD\)và \(\Delta BDC\)có:
CD chung
\(\widehat {ACD} = \widehat {BDC}\)
AC = BD (gt)
\( \Rightarrow \Delta ACD = \Delta BDC(c.g.c)\)
\( \Rightarrow \widehat {ADC} = \widehat {BCD}\) (2 góc tương ứng)
d, Hình thang ABCD (AB//CD) có \(\widehat {ADC} = \widehat {BCD}\)nên hình thang ABCD là hình thang cân.
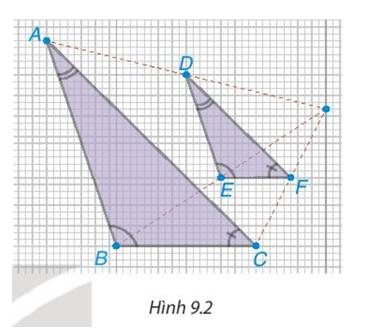



Ta có: \(\frac{{AB}}{{DE}} = 2{;^{}}\frac{{BC}}{{EF}} = 2{;^{}}\frac{{AC}}{{DF}} = 2\)
Ta có:\(\dfrac{AB}{DE}=2;\dfrac{BC}{EF}=2;\dfrac{AC}{DF}=2\)