Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Có \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{2}{3}\)
- Có \(\frac{{B'C'}}{{BC}} = \frac{2}{3}\)
- Tam giác A'B'C' có đồng dạng với tam giác ABC và đồng dạng với tỉ số \(\frac{2}{3}\)

Xét hai tam giác vuông HBA và tam giác vuông HDC nhận thấy:
\(\frac{{AB}}{{C{\rm{D}}}} = \frac{{AH}}{{CH}} = \frac{2}{3}\)
=> Hai tam giác đồng dạng
\( \Rightarrow \widehat {AB{\rm{D}}} = \widehat {C{\rm{D}}B}\)

a) Vì ABCD là hình bình hành nên AB // CD; AD // BC.
Suy ra \(\widehat {BAC} = \widehat {AC{\rm{D}}};\widehat {BCA} = \widehat {DAC}\)(hai góc so le trong).
Xét ∆ABC và ∆CDA có:
\(\widehat {BAC} = \widehat {AC{\rm{D}}}\) (chứng minh trên);
Cạnh AC chung.
\(\widehat {BCA} = \widehat {DAC}\) (chứng minh trên);
Do đó ∆ABC = ∆CDA (g.c.g).
Suy ra AB = CD, AD = BC (các cặp cạnh tương ứng); \(\widehat {ABC} = \widehat {C{\rm{D}}A}\) (hai góc tương ứng).
b) Xét ∆ABD và ∆CDB có:
AB = CD (chứng minh trên);
AD = BC (chứng minh trên);
Cạnh BD chung.
Do đó ∆ABD = ∆CDB.
Suy ra \(\widehat {DAB} = \widehat {BC{\rm{D}}}\) (hai góc tương ứng).
c) Xét ∆AOB và ∆COD có:
\(\widehat {BAC} = \widehat {AC{\rm{D}}}\) (chứng minh trên);
AB = CD (chứng minh trên);
\(\widehat {BCA} = \widehat {DAC}\) (chứng minh trên);
Do đó ∆AOB = ∆COD (g.c.g).
Suy ra OA = OC, OB = OD (các cặp cạnh tương ứng).

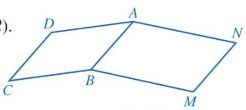
a, Do ABCD là hình bình hành: AB = CD.
Do ABMN là hình bình hành: AB = MN
Suy ra: CD = MN = AB
b, Do ABCD là hình bình hành \( \Rightarrow \widehat {BCD} = \widehat {DAB}\)
Do ABMN là hình bình hành \( \Rightarrow \widehat {BMN} = \widehat {NAB}\)
\(\widehat {BCD} + \widehat {BMN} = \widehat {DAB} + \widehat {NAB} = \widehat {DAN}\)

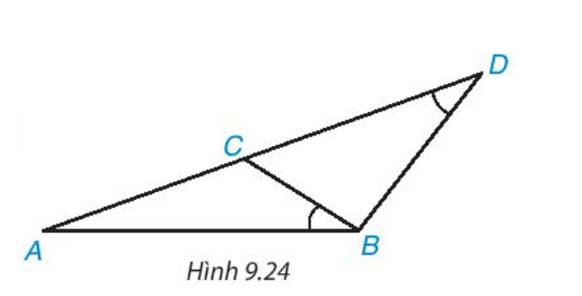
a) Xét tam giác \(ABD\) và tam giác \(ACB\) có:
\(\widehat {ABD} = \widehat {ACB}\) (giả thuyết)
\(\widehat A\) chung
Suy ra, \(\Delta ABD\backsim\Delta ACB\) (g.g)
b) Vì \(\Delta ABD\backsim\Delta ACB\)
Suy ra, \(\frac{{AB}}{{AC}} = \frac{{AD}}{{AB}}\) (các cặp cạnh tương ứng có cùng tỉ lệ).
Suy ra, \(A{B^2} = AC.AD = 9.4 = 36 \Rightarrow AB = \sqrt {36} = 6\)
Vậy \(AB = 6cm.\)

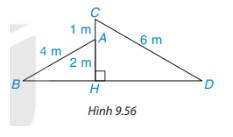
a, Xét \(\Delta ADC\)và \(\Delta BDC\)có:
DC là cạnh chung.
\(\widehat {ADC} = \widehat {BCD}\)(do ABCD là hình thang cân)
AD = BC
\( \Rightarrow \Delta ADC = \Delta BDC(c.g.c)\)
\( \Rightarrow \widehat {CAD} = \widehat {DBC}\)(2 góc tương ứng) hay
Do: \(\Delta ADC = \Delta BDC\)
Xét \(\Delta BAD\)và \(\Delta ACB\)có:
AB chung
AD = BC
AC = BD
\( \Rightarrow \Delta BDA = \Delta ACB\) (c.c.c)
\( \Rightarrow \widehat {BDA} = \widehat {ACB}\)(2 góc tương ứng) hay \(\widehat {TDA} = \widehat {TCB}\)
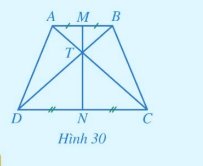
b, Xét \(\Delta TAD\)và \(\Delta TBC\)có:
\(\widehat {TAD} = \widehat {TBC}\)(theo câu a)
AD = BC (ABCD là hình thang cân)
\(\widehat {TDA} = \widehat {TCB}\)(theo câu a)
\( \Rightarrow \Delta TAD = \Delta TBC \Rightarrow TA = TB,TC = TD\)
c, Vì: TA = TB \( \Rightarrow \Delta ATB\)cân tại T suy ra TM là trung trực của AB
TC = TD \( \Rightarrow \Delta DTC\)cân tại T suy ra TN là trung trực của CD
Mà: M, T, N thẳng hàng. Nên MN là đường trung trực của cả 2 đường thẳng AB và CD

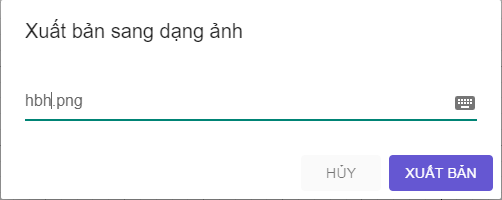
a) Dùng 

b) Lưu hình vẽ ở HĐ2 thành tệp hbh.png.
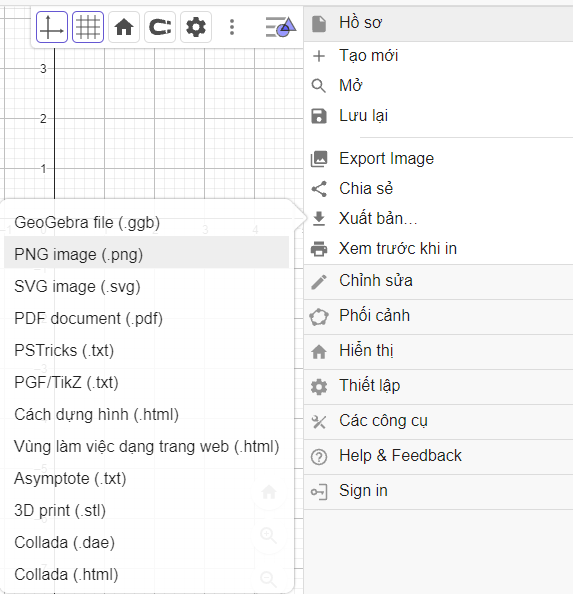
Vào Hồ sơ → Chọn Xuất bản → Chọn PNG image (.png).
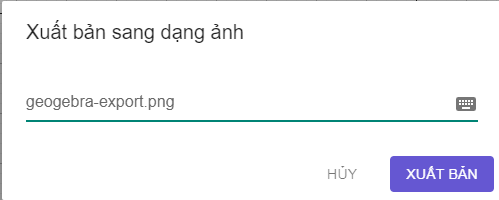
Ta đổi tên tệp thành hbh (như hình vẽ), sau đó chọn xuất bản.
Bước 1. Vẽ đoạn thẳng AB và có độ dài 4 cm tương tự như Bước 1 của HĐ1.
Bước 2. Vẽ điểm C sao cho BC = 4 cm.
Chọn công cụ 

Chọn công cụ 

Chọn công cụ 

Chọn công cụ 

Chọn công cụ 
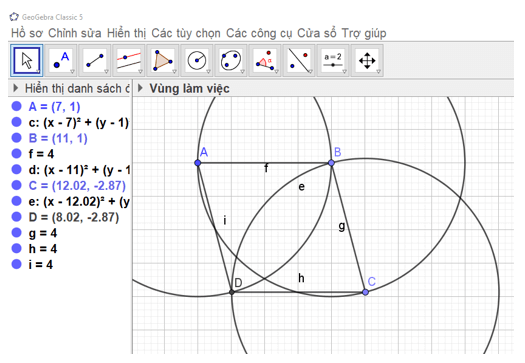
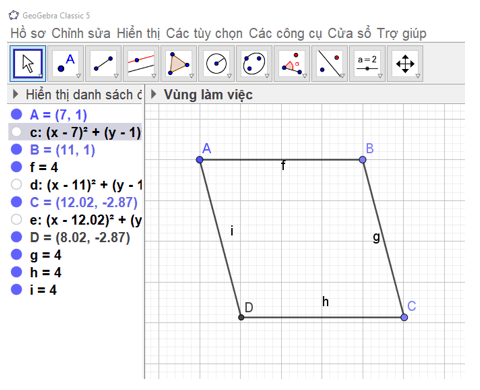
Bước 3. Ẩn đường tròn và thu được hình thoi ABCD.

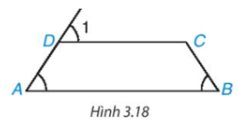
Ta có \(\widehat A = \widehat {{D_1}}\) mà hai góc này ở vị trí đồng vị nên AB // CD.
Suy ra tứ giác ABCD là hình thang.
Mặt khác hình thang ABCD có \(\widehat A = \widehat B\) nên ABCD là hình thang cân.
Do đó AD = BC (đpcm).

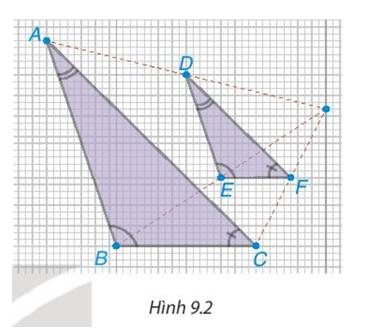
Ta có: \(\frac{{AB}}{{DE}} = 2{;^{}}\frac{{BC}}{{EF}} = 2{;^{}}\frac{{AC}}{{DF}} = 2\)
Ta có:\(\dfrac{AB}{DE}=2;\dfrac{BC}{EF}=2;\dfrac{AC}{DF}=2\)



 trong công cụ
trong công cụ  để kiểm tra trung điểm AC và BD có trùng nhau không.
để kiểm tra trung điểm AC và BD có trùng nhau không.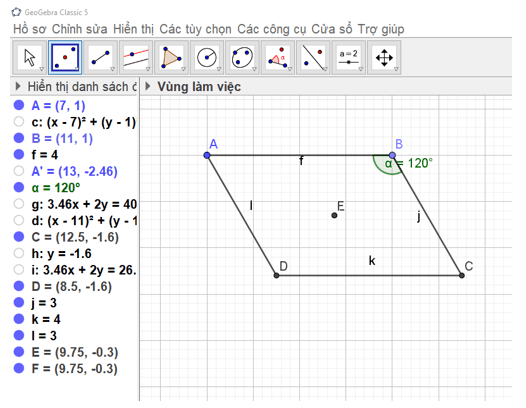
Xét tam giác ABC và tam giác ADB có
\(\widehat {ABC} = \widehat {A{\rm{D}}B}\) và \(\widehat A\) chung
=> ΔABC ∽ ΔADB (g.g)
=> \(\frac{{AB}}{{AD}} = \frac{{AC}}{{AB}}\)
=> \(A{B^2} = A{\rm{D}}.AC\)