Question

[Quoc Tran Anh Le]

Trong Hình 76, cho biết các tam giác ABD và BCE là tam giác đều và A, B, C thẳng hàng. Chứng minh rằng:

a) AD // BE và BD // CE;

b) \(\widehat {ABE} = \widehat {DBC} = 120^\circ \);

c) AE = CD.

Answer 1

[Hà Quang Minh]

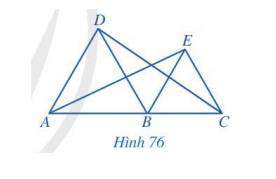
a)

Tam giác ABD và BCE là tam giác đều nên \(\widehat {EBC} = \widehat {DAB} = 60^\circ \) và A, B, C thẳng hàng. Hai góc EBC và DAB ở vị trí đồng vị nên AD // BE.

Tam giác ABD và BCE là tam giác đều nên \(\widehat {DBA} = \widehat {ECB} = 60^\circ \) và A, B, C thẳng hàng. Hai góc DBA và ECB ở vị trí đồng vị nên BD // CE.

b) Ta có A, B, C thẳng hàng nên góc ABC bằng 180°. Mà \(\widehat {DBA} = \widehat {EBC} = 60^\circ  \Rightarrow \widehat {DBE} = 60^\circ \).

Vậy \(\widehat {ABE} = \widehat {DBC} = 120^\circ \) (\(\widehat {ABE} = \widehat {DBA} + \widehat {DBE};\widehat {DBC} = \widehat {DBE} + \widehat {EBC}\)).

c) Tam giác ABD và BCE là tam giác đều 

\(\Rightarrow AB=AD, BE=BC\)

Xét hai tam giác ABE và DBC có:

     AB = DB;

     \(\widehat {ABE} = \widehat {DBC} = 120^\circ \);

     BE = BC.

\(\Rightarrow \Delta ABE = \Delta DBC\) (c.g.c)

Do đó, AE = DC ( 2 cạnh tương ứng).