Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đoạn thẳng AB có hướng được gọi là vecto \(\overrightarrow {AB} \).

Xét tam giác CDB, ta có: CD = 441, CB = 575 và DB = 538 (đơn vị: m)
Và nửa chu vi là: \(\frac{{441 + 575 + 538}}{2} = 777(m)\)
Do đó: \({S_{CDB}} = \sqrt {777.\left( {777 - 441} \right).\left( {777 - 575} \right).\left( {777 - 538} \right)} \approx 112267,7\left( {{m^2}} \right)\)
Xét tam giác DBE, ta có: DE = 217, EB = 476 và DB = 538 (đơn vị: m)
Và nửa chu vi là: \(\frac{{217 + 476 + 538}}{2} = 615,5(m)\)
Do đó: \({S_{DBE}} = \sqrt {615,5.\left( {615,5 - 217} \right).\left( {615,5 - 476} \right).\left( {615,5 - 538} \right)} \approx 51495,13\left( {{m^2}} \right)\)
Xét tam giác ABE, ta có: AE = 401, EB = 476 và BA =256 (đơn vị: m)
Và nửa chu vi là: \(\frac{{401 + 476 + 256}}{2} = 566,5(m)\)
Do đó: \({S_{ABE}} = \sqrt {566,5.\left( {566,5 - 401} \right).\left( {566,5 - 476} \right).\left( {566,5 - 256} \right)} \approx 51327,97\left( {{m^2}} \right)\)
Vậy diện tích S của ngũ giác ABCDE là: \(S = {S_{CDB}} + {S_{DBE}} + {S_{ABE}} \approx 112267,7 + 51495,13 + 51327,97 = 215090,8\left( {{m^2}} \right)\)
Chú ý
+) Để tính diện tích ngũ giác ABCDE thông qua các tam giác nhỏ, ta cần chọn các tam giác thỏa mãn: “phần trong của chúng không đè lên nhau” và “ghép lại vừa khít tạo thành ngũ giác ABCDE”
+) Ưu tiên tính thông qua các tam giác đã biết đủ các cạnh.

Gắn hệ trục Oxy vào chiếc cổng, gọi chiều cao của cổng là h ta vẽ lại parabol như dưới đây:
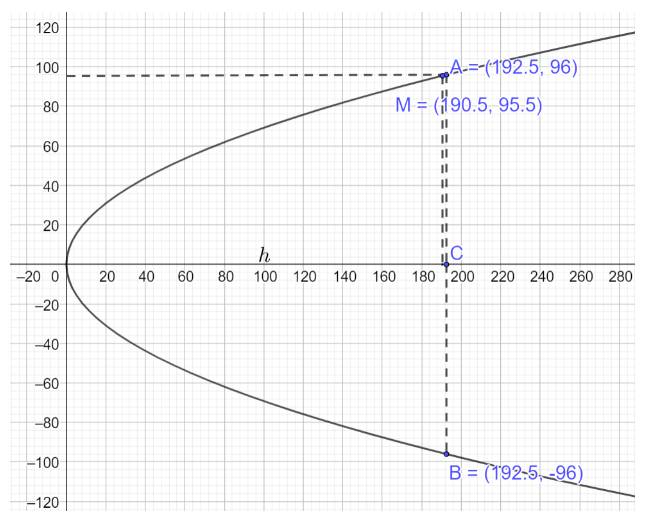
Phương trình parabol mô phỏng cổng có dạng \({y^2} = 2px\)
Theo giả thiết \(AB = 2{y_A} = 192 \Rightarrow {y_A} = 96,OC = h \Rightarrow M\left( {h - 2;95,5} \right),A\left( {h;96} \right)\)
Thay tọa độ các điểm \(M\left( {h - 2;95,5} \right),A\left( {h;96} \right)\) vào phương trình \({y^2} = 2px\) ta có:
\(\left\{ \begin{array}{l}95,{5^2} = 2p\left( {h - 2} \right)\\{96^2} = 2ph\end{array} \right. \Rightarrow \left\{ \begin{array}{l}p = \frac{{383}}{{16}}\\h \simeq 192,5\end{array} \right.\)
Vậy chiều cao của cổng gần bằng 192,5 m

Tổng các tích nhân được bằng với kết quả khai triển của tích (a+b).(c+d)= a.c + a.d + b.c + b.d

Bước 1:
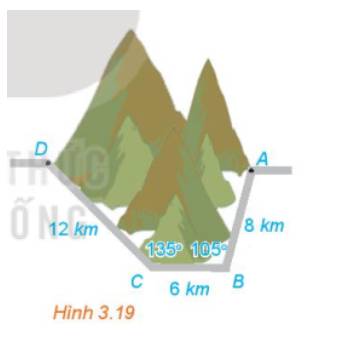
Áp dụng định lí cos trong tam giác ABC ta có:
\(\begin{array}{l}A{C^2} = {6^2} + {8^2} - 2.6.8.\cos {105^o}\\ \Rightarrow AC \approx 11,1735\;(km)\end{array}\)
Bước 2:
Lại có: Theo định lí sin thì
\(\begin{array}{l}\frac{{AB}}{{\sin ACB}} = \frac{{AC}}{{\sin ABC}} \Rightarrow \sin ACB = \frac{{8.\sin {{105}^o}}}{{11,1735}}\\ \Rightarrow \widehat {ACB} \approx 44^o\\ \Rightarrow \widehat {ACD} = {135^o} - 44^o = 91^o\end{array}\)
Bước 3:
Áp dụng định lí cos trong tam giác ACD ta có:
\(\begin{array}{l}A{D^2} = {12^2} + 11,{1735^2} - 2.12.11,1735\cos 91^o\\ \Rightarrow AD \approx 16,5387\;(km)\end{array}\)
Bước 4:
Độ dài đường mới giảm số kilomet so với đường cũ là: \(12 + 6 + 8 - 16,5387 = 9,4613\;(km)\)

Tham khảo:
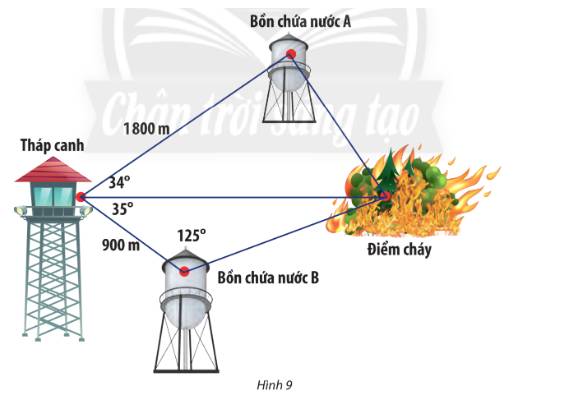
Đặt các điểm A, B, C, D lần lượt là vị trí bồn chứa nước A, bồn chứa nước B, tháp canh và đám cháy.
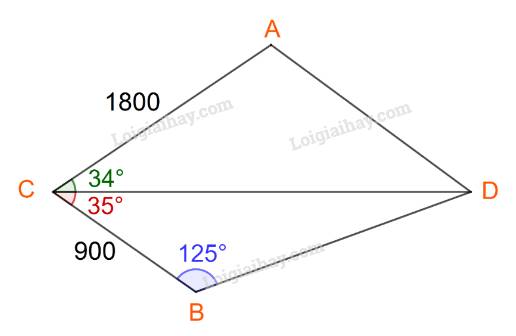
Ta có: \(CB = 900,\;\widehat {CDB} = {180^o} - ({125^o} + {35^o}) = {20^o}\)
Áp dụng định lí sin trong tam giác CBD, ta có:
\(\frac{{CB}}{{\sin D}} = \frac{{BD}}{{\sin C}} = \frac{{CD}}{{\sin B}}\)
Suy ra:
\(BD = \frac{{CB.\sin C}}{{\sin D}} = \frac{{900.\sin {{35}^o}}}{{\sin {{20}^o}}} \approx 1509,3\)
\(CD = \frac{{CB.\sin B}}{{\sin D}} = \frac{{900.\sin {{125}^o}}}{{\sin {{20}^o}}} = 2155,5\)
Áp dụng định lí cosin trong tam giác ACD ta có:
\(\begin{array}{l}A{D^2} = A{C^2} + C{D^2} - 2.AC.CD.\cos \widehat {ACD}\\ \Leftrightarrow A{D^2} = {1800^2} + 2155,{5^2} - 2.1800.2155,5.\cos {34^o} \approx 1453014,5\\ \Leftrightarrow AD \approx 1205,4\end{array}\)
Vì \(AD < BD\) nên khoảng cách từ bồn chứa nước A đến đám cháy là ngắn hơn.
Vậy nên dẫn nước từ bồn chứa nước A để dập tắt đám cháy nhanh hơn.
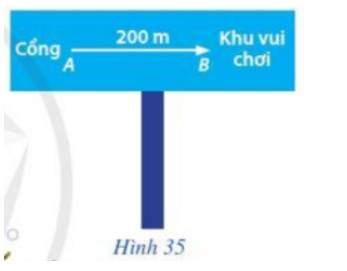




Hình ảnh về mũi tên chỉ dẫn cho biết:
+) Hướng đi từ Cổng đến Khu vui chơi: Đi sang phải
+) Khoảng cách từ Cổng đến Khu vui chơi: 200 m.