Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tam thức f(x) = -2x2 + 3x + 5 có hai nghiệm là – 1 và 5/2 ; hệ số a= - 2 < 0.
Do đó, với -1 < x < 5/2 thì f(x) trái dấu với hệ số của x2

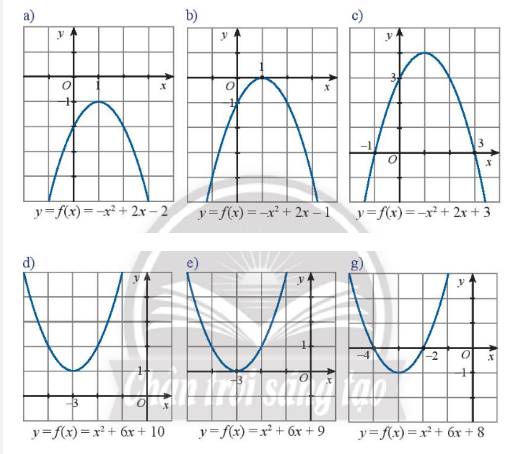
a) Dựa vào đồ thị ta thấy hàm số đã cho vô nghiệm
Biệt thức \(\Delta = {2^2} - 4.\left( { - 1} \right).\left( { - 2} \right) = - 4 < 0\)
Ta thấy hệ số của \({x^2}\) là \( - 1 < 0\)
Đồ thị nằm dưới trục hoành với mọi x
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với \(\forall x \in \mathbb{R}\)
b) Dựa vào đồ thị ta thấy hàm số đã cho có nghiệm kép \({x_1} = {x_2} = 1\)
Biệt thức \(\Delta = {2^2} - 4.\left( { - 1} \right).\left( { - 1} \right) = 0\)
Ta thấy hệ số của \({x^2}\) là \( - 1 < 0\)
Đồ thị nằm dưới trục hoành với mọi x
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với \(\forall x \in \mathbb{R}\)
c) Dựa vào đồ thị ta thấy hàm số đã cho có hai nghiệm phân biệt \({x_1} = - 1;{x_2} = 3\)
Biệt thức \(\Delta = {2^2} - 4.\left( { - 1} \right).3 = 16 > 0\)
Ta thấy hệ số của \({x^2}\) là \( - 1 < 0\)
Đồ thị nằm dưới trục hoành khi \(x \in \left( { - \infty , - 1} \right) \cup \left( {3, + \infty } \right)\)
Đồ thị nằm trên trục hoành với mọi \(x \in \left( { - 1,3} \right)\)
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) khi \(x \in \left( { - \infty , - 1} \right) \cup \left( {3, + \infty } \right)\)
d) Dựa vào đồ thị ta thấy hàm số bậc hai đã cho vô nghiệm
Biệt thức \(\Delta = {6^2} - 4.1.10 = - 4 < 0\)
Ta thấy hệ số của \({x^2}\) là \(1 > 0\)
Đồ thị nằm trên trục hoành với mọi \(x\)
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với mọi \(x \in \mathbb{R}\)
e) Dựa vào đồ thị ta thấy hàm số đã cho có nghiệm kép \({x_1} = {x_2} = - 3\)
Biệt thức \(\Delta = {6^2} - 4.1.9 = 0\)
Ta thấy hệ số của \({x^2}\) là \(1 > 0\)
Đồ thị nằm trên trục hoành với mọi x
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với mọi \(x \in \mathbb{R}\)
g) ) Dựa vào đồ thị ta thấy hàm số đã cho có hai nghiệm phân biệt \({x_1} = - 4;{x_2} = - 2\)
Biệt thức \(\Delta = {6^2} - 4.1.8 = 4 > 0\)
Ta thấy hệ số của \({x^2}\) là \(1 > 0\)
Đồ thị nằm trên trục hoành khi \(x \in \left( { - \infty , - 4} \right) \cup \left( { - 2, + \infty } \right)\)
Đồ thị nằm dưới trục hoành với mọi \(x \in \left( { - 4, - 2} \right)\)
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) khi \(x \in \left( { - \infty , - 4} \right) \cup \left( { - 2, + \infty } \right)\)

-2x + 3 > 0 ⇔ -2x > -3 ⇔ x < 3/2
Biểu diễn tập nghiệm trên trục số:
Nhị thức f(x) = -2x + 3 có giá trị:
Trái dấu với hệ số của x khi x < 3/2
Cùng dấu với hệ số của x khi x > 3/2

a) Ta có: \(f\left(x\right)=x\left(x^2+x-2\right)=x\left(x-1\right)\left(x+2\right)\)
Lập bảng xét dấu

Vậy để \(f\left(x\right)>0\) \(\Leftrightarrow x\in\left(-2;0\right)\cup\left(1;+\infty\right)\)
b) Ta có: \(\left(3x^2+7x-6\right)\left(5x+8\right)^2\le0\)
\(\Leftrightarrow3x^2+7x-6\le0\) \(\Leftrightarrow-3\le x\le\dfrac{2}{3}\)
Vậy \(x\in\left[-3;\dfrac{2}{3}\right]\)

Bài 2:
a: =>2x^2-4x+1=x^2+x+5
=>x^2-5x-4=0
=>\(x=\dfrac{5\pm\sqrt{41}}{2}\)
b: =>11x^2-14x-12=3x^2+4x-7
=>8x^2-18x-5=0
=>x=5/2 hoặc x=-1/4

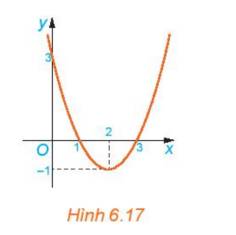
a) Hệ số a là: a=1
\(f(0) = {0^2} - 4.0 + 3 = 3\)
\(f(1) = {1^2} - 4.1 + 3 = 0\)
\(f(2) = {2^2} - 4.2 + 3 = - 1\)
\(f(3) = {3^2} - 4.3 + 3 = 0\)
\(f(4) = {4^2} - 4.4 + 3 = 3\)
=> f(0); f(4) cùng dấu với hệ số a; f(2) khác dấu với hệ số a
b) Nhìn vào đồ thị ta thấy
- Trên khoảng \(\left( { - \infty ;1} \right)\) đồ thị nằm phía trên trục hoành
- Trên khoảng \(\left( {1;3} \right)\), đồ thị nằm phía dưới trục hoành
- Trên khoảng \(\left( {3; + \infty } \right)\), đồ thị nằm phía trên trục hoành
c) - Trên khoảng \(\left( { - \infty ;1} \right)\) đồ thị nằm phía trên trục hoành => f(x)>0, cùng dầu với hệ số a
- Trên khoảng \(\left( {1;3} \right)\), đồ thị nằm phía dưới trục hoành => f(x) <0, khác dấu với hệ số a
- Trên khoảng \(\left( {3; + \infty } \right)\), đồ thị nằm phía trên trục hoành => f(x)>0, cùng dấu với hệ số a

a: Để phương trình có hai nghiệm trái dấu thì m+2<0
hay m<-2

Tam thức g(x) = -3x2 + 7x – 4 có hai nghiệm là 1 và 4/3 , hệ số a= - 3 < 0
Do đó, với x < 1 hoặc x > 4/3 thì g(x) cùng dấu với hệ số của x2