Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: pi/2<a<pi
=>sin a>0
\(sina=\sqrt{1-\left(-\dfrac{1}{\sqrt{3}}\right)^2}=\dfrac{\sqrt{2}}{\sqrt{3}}\)
\(sin\left(a+\dfrac{pi}{6}\right)=sina\cdot cos\left(\dfrac{pi}{6}\right)+sin\left(\dfrac{pi}{6}\right)\cdot cosa\)
\(=\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{2}}{\sqrt{3}}+\dfrac{1}{2}\cdot-\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{6}-2}{2\sqrt{3}}\)
b: \(cos\left(a+\dfrac{pi}{6}\right)=cosa\cdot cos\left(\dfrac{pi}{6}\right)-sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}-\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}-\sqrt{2}}{2\sqrt{3}}\)
c: \(sin\left(a-\dfrac{pi}{3}\right)\)
\(=sina\cdot cos\left(\dfrac{pi}{3}\right)-cosa\cdot sin\left(\dfrac{pi}{3}\right)\)
\(=\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}+\dfrac{1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}=\dfrac{\sqrt{2}+\sqrt{3}}{2\sqrt{3}}\)
d: \(cos\left(a-\dfrac{pi}{6}\right)\)
\(=cosa\cdot cos\left(\dfrac{pi}{6}\right)+sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}+\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}+\sqrt{2}}{2\sqrt{3}}\)


sin π/6 = 1/2; cos π/6 = √3/2
sin π/4 = √2/2; cos π/4 = √2/2
sin 1,5 = 0,9975; cos 1,5 = 0,0707
sin 2 = 0,9093; cos 2 = -0,4161
sin 3,1 = 0,0416; cos 3,1 = -0,9991
sin 4,25 = -0,8950; cos 4,25 = -0,4461
sin 5 = -0,9589; cos 5 = 0,2837

\(A=cos\left(\alpha+\dfrac{\pi}{6}\right)cos\left(\alpha-\dfrac{\pi}{6}\right)=\dfrac{1}{2}\left[cos\left(\alpha+\dfrac{\pi}{6}+\alpha-\dfrac{\pi}{6}\right)+cos\left(\alpha+\dfrac{\pi}{6}-\alpha+\dfrac{\pi}{6}\right)\right]\)
\(=\dfrac{1}{2}\left(cos2\alpha+cos\dfrac{\pi}{3}\right)=\dfrac{1}{2}\left(\dfrac{1}{4}+\dfrac{1}{2}\right)=\dfrac{3}{8}\)


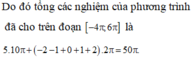
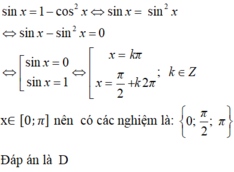
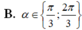
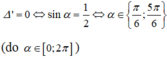
Chọn B