
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Trả lời:
Tam giác ABC có:
Sin B = AC/BC (hệ thức lượng)
=> AC = Sin B.BC = Sin 450 . 10 = 5√2 (cm)
Sin C = AB/BC
=> AB = Sin 300 . 10 = 5 (cm)
Ta có tam giác ABC có: góc A + góc B + góc C = 1800
=> góc A = 1800 - 450 - 300 = 1050
Tam giác ABC có: Sin B = (hệ thức lượng) => AC = Sin B.BC = Sin 450 . 10 = (cm)
Sin C = (hệ thức lượng) => AB = Sin 300 . 10 = 5 (cm)
Ta có tam giác ABC có: góc A + góc B + góc C = 1800 (định lý)
=> góc A = 1800 - 450 - 300 = 1050

Câu 1: Cả 4 câu đều đúng
Câu 2:
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=3^2+4^2=25\)
=>BC=5
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot5=3\cdot4=12\)
=>AH=2,4

Ta có:
2 tia phân giác ngoài và trong tạo với nhau 1 góc bằng 90 độ
=> \(\widehat{DBE}=90^o\)
Áp dụng định lý Pytago vào tam giác DAB
=> \(DB=\sqrt{AB^2+AD^2}=2\sqrt{5}cm\)
ÁP dụng hệt thức lượng vào tam giác vuông DBE
=> \(DB^2=DA.DE\Rightarrow DE=\dfrac{DB^2}{AD}=\dfrac{\left(2\sqrt{5}\right)^2}{2}=10cm\)

Lời giải:
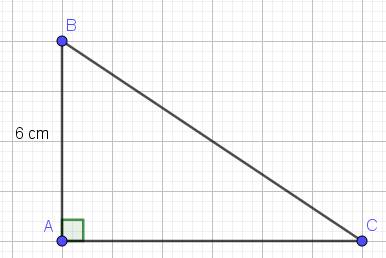
Có: $\frac{3}{5}=\cos C = \frac{AC}{BC}$
$\Rightarrow BC=\frac{5}{3}AC$
Áp dụng định lý Pitago:
$AB^2+AC^2=BC^2$
$\Rightarrow 6^2+AC^2=(\frac{5}{3}AC)^2$
$\Rightarrow 36=(\frac{5}{3}AC)^2-AC^2=\frac{16}{9}AC^2$
$\Rightarrow AC=4,5$ (cm)
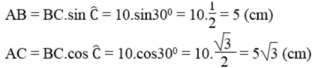
\(AC=10\cdot tan\left(30^o\right)=\dfrac{10\sqrt{3}}{3}\)