
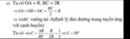
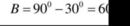


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


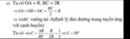
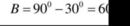



Câu c,
+ Gọi K là trung điểm của BH
+ Chứng minh IK vuông góc với BM
+ K là trực tâm tam giác BMI
+ Chứng minh KM// EI
+ Chứng minh M là trung điểm của BE (t/c đường trung bình)

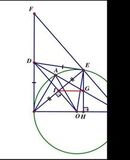
a: Xét (O) có
ΔABC nội tiêp
BC là đường kính
Do đó: ΔABC vuông tại A
Xét ΔABC vuông tại A có sin ACB=AB/BC=1/2
nên góc ACB=30 độ
=>góc ABC=60 độ
b: Xét (O) có
DB,DE là các tiếp tuyến
nên DB=DE
mà OB=OE
nên OD là trung trực của BE
=>OD vuông góc với BE
=>DI*DO=DB^2
Xét ΔDBA và ΔDCB có
góc DBA=góc DCB
góc D chung
Do đó: ΔDBA đồng dạng với ΔDCB
=>DB/DC=DA/DB
=>DB^2=DC*DA=DI*DO

a: Xét (O) có
ΔABC nội tiếp
BC là đường kính
Do đó: ΔABC vuông tại A
Xét ΔBCA vuông tại A có sin ACB=AB/BC=1/2
nên góc ACB=30 độ
=>góc ABC=60 độ
b: Xét (O) có
DB,DE là các tiếp tuyến
nên DB=DE
mà OB=OE
nên OD là đường trung trực của BE
=>OD vuông góc với BE
DI*DO=DB^2
DA*DC=DB^2
Do đó: DI*DO=DA*DC