Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có $\lambda =24cm $
Bạn vẽ hình ra .
Đoạn AB =24cm sau đó vẽ 2 bụng sóng.
Lấy M N nằm giữa sao cho MN= AB/3 = 8 cm.
Khoảng cách MN lớn nhất khi chúng nằm trên bụng và nhỏ nhất khi duỗi thẳng.
Ta có $\dfrac{MN_{lớn}}{MN_{nhỏ}} =1.25 \rightarrow MN_{lớn}=10 \rightarrow $biên độ của M và N là 3cm.
Khoảng cách từ M đến nút bằng 4cm =$\dfrac{\lambda}{6} \rightarrow A_{bụng} =2\sqrt{3}$
Đây em nhé Câu hỏi của Nguyễn Thị Trúc Đào - Vật lý lớp 12 | Học trực tuyến
Đáp án A
+ Khi xảy ra sóng dừng trên dây có 20 bụng sóng
+ Biên độ dao động của các phần tử dây cách nút A một đoạn d được xác định bằng biểu thức:
với 
là biên độ của điểm bụng
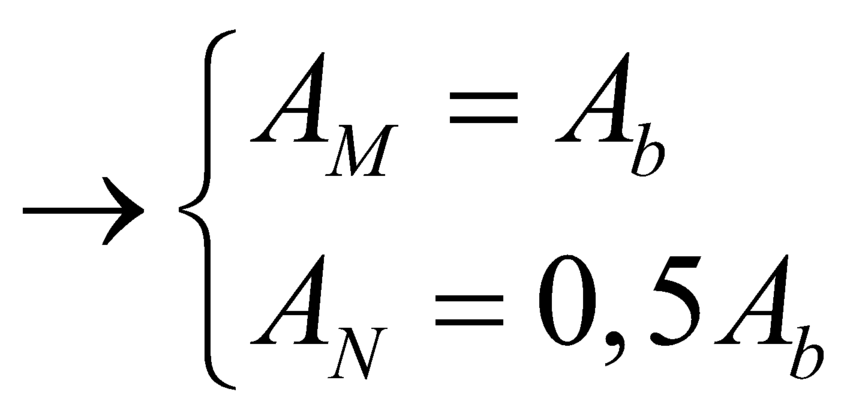
+ Theo giả thuyết của bài toán
Đáp án D
+ Bước sóng của sóng λ = v f = 4 c m .
+ Điểm bụng dao động với biên độ A =2cm, điểm M dao động với biên độ A M = 3 2 A b
M cách bụng một khoảng λ 12 = 1 3 c m
Lưu ý rằng M N = λ + λ 12 = 13 3 c m
Biểu diễn vị trí của M và N trên dây (lưu ý rằng cả M và N đều không phải bụng)
→ A N = 2 c m .
+ M và N dao động cùng pha nhau: