Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử ∆A'B'C' ∽ ∆ABC, hiệu độ dài tương ứng của A'B' và AB là 12,5.
Ta có: = mà =
=> = => = = = = 6,25 cm
Giả sử ∆A'B'C' ∽ ∆ABC, hiệu độ dài tương ứng của A'B' và AB là 12,5.
Ta có: CABCCA′B′C′CABCCA′B′C′CABCCA′B′C′= 151715171517 mà CABCCA′B′C′CABCCA′B′C′CABCCA′B′C′ = ABA′B′ABA′B′ABA′B′
=> 151715171517 = ABA′B′ABA′B′ABA′B′ => AB15AB15AB15 = A′B′17A′B′17A′B′17 = A′B′−AB17−15A′B′−AB17−15A′B′−AB17−15 = 12.5212.5212.52 = 6,25 cm

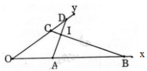
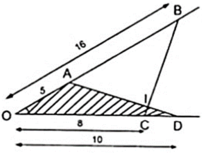
a, Ta có :
\(\frac{OA}{OC}=\frac{5}{8};\frac{OB}{OD}=\frac{10}{16}=\frac{5}{8}\)
\(\Rightarrow\frac{OA}{OC}=\frac{OB}{OD}\)
Mà góc O chung nên \(\Delta OCB~\Delta OAD\)( trường hợp 2 )
b, \(\Delta ICD , \Delta IAB\)có :
\(\widehat{CID}=\widehat{AIB}\)( đối đỉnh )
\(\widehat{CDI}=\widehat{IBA} \left(do \Delta OCB~\Delta OAD\right)\)
\(\Rightarrow\widehat{DCI}=\widehat{BAI}\)( tổng 3 góc trong tam giác )
Vậy : Hai tam giác IAB và ICD có các góc = nhau từng đôi 1


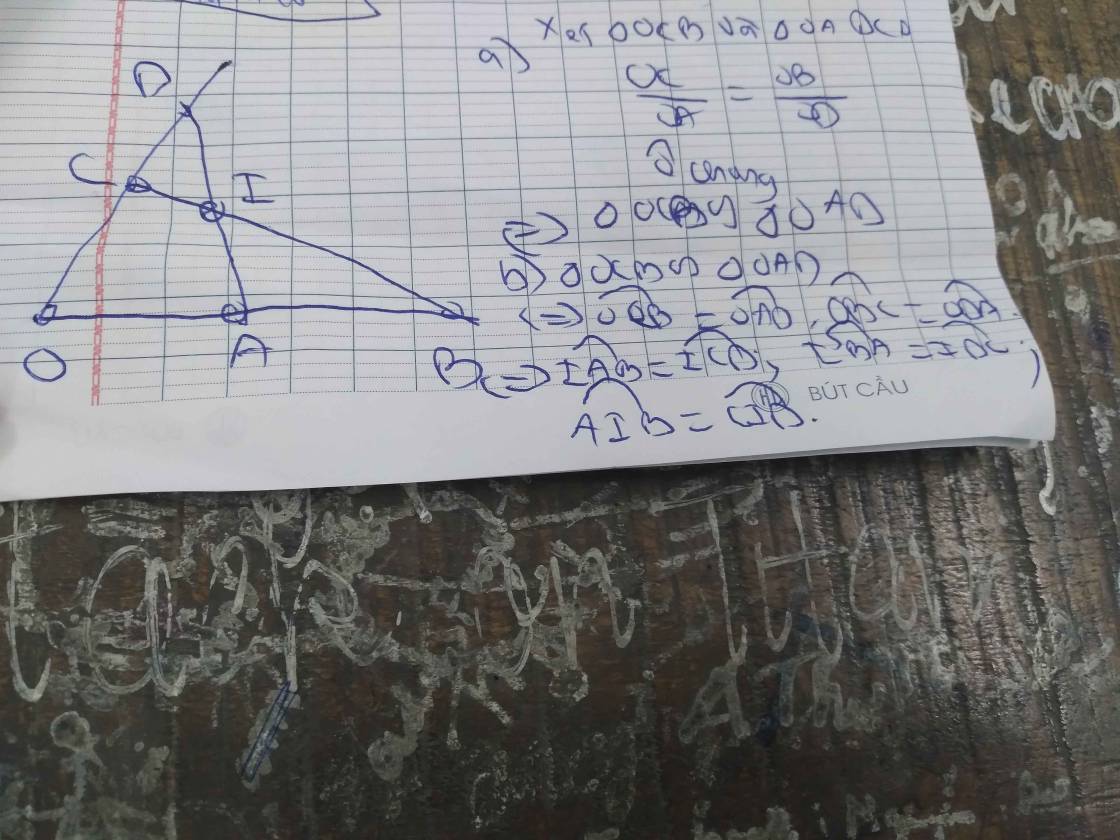




a)Ta có:
\(\dfrac{OA}{OC}=\dfrac{5}{8};\dfrac{OD}{OB}=\dfrac{10}{16}=\dfrac{5}{8}\)
\(\Rightarrow\dfrac{OA}{OC}=\dfrac{OD}{OB}\)
Mà có O là góc chung nên \(\Delta OCB\) đồng dạng với \(\Delta OAD\) (trường hợp 2)
b) ΔIAB và ΔICD có: ∠CID = ∠AIB (góc đối đỉnh) ∠ODA = ∠OBC (t/c) ⇒ ∠ICD = ∠IAB ( Định lí tổng 3 góc tam giác) .
Vậy ∠IAB và ICD có các góc bằng từng đôi một.