Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

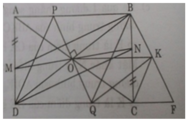
(a) Cho \(AD\cap BC=\left\{O\right\}.\) Do \(AB\left|\right|CD\left(gt\right)\Rightarrow\hat{OAB}=\hat{ODC}=\hat{OCD}=\hat{OBA}\) (đồng vị và tính chất hình thang cân) \(\Rightarrow\Delta OAB\) cân tại \(O\Rightarrow OA=OB.\)
Mà: \(AM=BN\Rightarrow OA+AM=OB+BN\Leftrightarrow OM=ON\Rightarrow\Delta OMN\) cân tại \(O\Rightarrow\hat{OMN}=\hat{ONM}=\dfrac{180^o-\hat{O}}{2}\left(1\right)\).
Lại có \(\Delta OAB\) cân tại \(O\left(cmt\right)\Rightarrow\hat{OAB}=\hat{OBA}=\dfrac{180^o-\hat{O}}{2}\left(2\right)\)
Từ (1) và (2), suy ra: \(\hat{OMN}=\hat{OAB}\Rightarrow AB\left|\right|MN\).
Mà: \(AB\left|\right|CD\left(gt\right)\Rightarrow AB\left|\right|MN\left|\right|CD\left(3\right)\)
Từ (1) và (3) \(\Rightarrow ABNM\) là hình thang cân (đpcm).
Mặt khác: \(\hat{MDC}=\hat{NCD}\left(gt\right)\left(4\right)\)
Từ (3) và (4) \(\Rightarrow MNCD\) là hình thang cân (đpcm).

a: ABCD là hình chữ nhật
=>\(AC^2=AB^2+AD^2\)
=>\(AC^2=256+81=337\)
=>\(AC=\sqrt{337}\left(cm\right)\)
b: Sửa đề: MA=NB
Xét ΔMAD vuông tại A và ΔNBC vuông tại B có
MA=NB
AD=BC
Do đó: ΔMAD=ΔNBC
=>\(\widehat{MDA}=\widehat{NCB}\)
\(\widehat{ADM}+\widehat{MDC}=90^0\)
\(\widehat{NCB}+\widehat{NCD}=90^0\)
mà \(\widehat{MDA}=\widehat{NCB}\)
nên \(\widehat{MDC}=\widehat{NCD}\)
Xét tứ giác MNCD có MN//CD và \(\widehat{MDC}=\widehat{NCD}\)
nên MNCD là hình thang cân

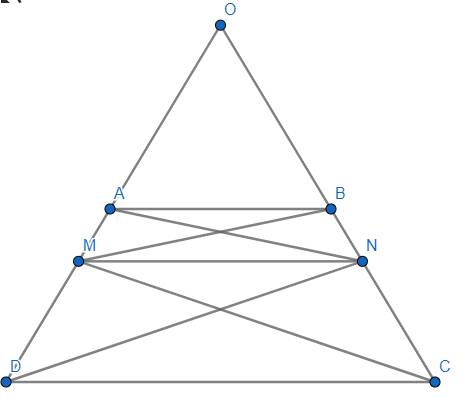
a) Ta có AD = BC; AD // BC (gt), AM = CN (gt)
⇒ AD – AM = BC – CN
Hay DM = BN
Lại có DM // BN
Do đó MNDN là hình bình hành ⇒ BM // DN
 cảm ơn bạn và cho mik hỏi là làm thế này có đc ko
cảm ơn bạn và cho mik hỏi là làm thế này có đc ko
Xét Δ ADM và Δ BNC ta có :
Góc A = Góc B = 90o (ABCD là HCN)
AD=BC (ABCD là HCN)
AM=BN (đề bài)
⇒ Δ ADM và Δ BNC (cạnh, góc, cạnh)
⇒ Góc ADM = Góc BCN
mà Góc ADM + Góc MDC =90o
Góc BCN + Góc NCD =90o
⇒ Góc MDC = Góc NCD
mà MN song song CD (AB song song CD)
⇒ MNCD là hình thang cân