TN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MH
20 tháng 1 2023
Áp dụng hệ thức vi ét:
\(\Rightarrow\left\{{}\begin{matrix}x_1+x_2=-m\\x_1.x_2=m-1\end{matrix}\right.\)
⇒ \(\left(x_1+x_2\right)^2-2x_1.x_2=m^2-2\left(m-1\right)\)
\(\Leftrightarrow x_1^2+x_2^2=\left(m-1\right)^2\)
\(Min\left(x_1^2+x_2^2=0\right)\Leftrightarrow m=1\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 12 2022
Thay \(x=-1\) vào ta được:
\(\left(-1\right)^2-\left(3m+1\right)\left(-1\right)+m-5=0\)
\(\Leftrightarrow4m-3=0\Rightarrow m=\dfrac{3}{4}\)
DT
23 tháng 4 2022
\(a.\Leftrightarrow mx^2+2mx-x+m+2=0\)
\(\Leftrightarrow mx\left(x+2\right)+\left(m+2\right)-x=0\)
\(\Leftrightarrow\left(m+2\right)\left(mx+1\right)-x=0\)
\(\Rightarrow\left\{{}\begin{matrix}m=\left(0+x\right):\left(mx+1\right)-2\\m=[\left(0+x\right):\left(m+2\right)-1]:x\end{matrix}\right.\)
29 tháng 3 2018
a) Ta có:Δ =(-7)2 -4.2.2 =49 -16 =33 >0
Phương trình có 2 nghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
x1 + x2 =-b/a =7/2 ;x1x2 =c/a =2/2 =1
b) c = -16 suy ra ac < 0
Phương trình có 2 ghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
x1 + x2 =-b/a =-2/5 ;x1x2 =c/a =-16/5
c) Ta có: Δ’ = 22 – (2 -√3 )(2 + √2 ) =4 -4 - 2√2 +2√3 +√6
= 2√3 - 2√2 +√6 >0
Phương trình 2 ghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
d) Ta có : Δ = (-3)2 -4.1,4.1,2 =9 – 6,72 =2,28 >0
Phương trình có 2 ghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
x1 + x2 = -b/a = 3/(1.4) = 30/14 = 15/7 ; x1x2 = c/a = (1.2)/(1.4) = 12/14 = 6/7
Ta có: Δ = 12 -4.5.2 = 1 - 40 = -39 < 0
21 tháng 6 2023
Theo đề, ta có:
-2(-3)^2+(m-1)*(-3)+m=0
=>-3m+3+m-2*9=0
=>-2m-15=0
=>m=-15/2
PT khi đó sẽ là -2x^2+(-17/2)x-15/2=0
=>2x^2+17/2x+15/2=0
=>x=-5/4
Tổng các nghiệm là -5/4-3=-17/4
A
8 tháng 6 2023
a) Để phương trình có 2 nghiệm phân biệt
<=> \(\Delta=\left[-\left(4m+3\right)^2\right]-4.2.\left(2m-1\right)=16m^2+24m+9-16m+8=16m^2+8m+1+16=\left(4m+1\right)^2+16>0\)
với mọi giá trị của m.
Vậy phương trình luôn có 2 nghiệm phân biệt với mọi giá trị của m.
b) Vì phương trình luôn có 2 nghiệm phân biệt với mọi giá trị của m nên ta có: x1+x2= \(\dfrac{4m+3}{2}\)và x1.x2=\(\dfrac{2m-1}{2}\)
A
2
H
3 tháng 5 2023
Đặt \(x^2=t\) \(\left(t\ge0\right)\)
\(\Rightarrow t^2-2t-3=0\\ \Leftrightarrow\Delta=\left(-2\right)^2-4.1.\left(-3\right)=16\\ \Rightarrow\left\{{}\begin{matrix}t_1=\dfrac{2+\sqrt{16}}{2.1}=3\\t_2=\dfrac{2-\sqrt{16}}{2}=-1\end{matrix}\right.\)
\(\Rightarrow t=3\) vì \(t\ge0\)
\(\Rightarrow x^2=3\\ \Rightarrow\begin{matrix}x=\sqrt{3}\\x=-\sqrt{3}\end{matrix}\)
KV
3 tháng 5 2023
Đặt t = x² (t ≥ 0)
Phương trình tương đương:
t² - 2t - 3 = 0
Ta có: a - b + c = 1 - (-2) - 3 = 0
Phương trình có hai nghiệm:
t₁ = -1 (loại)
t₂ = 3 (nhận)
Với t₂ = 3
⇔ x² = 3
⇔ x = √3; x = -√3
Vậy S = {-√3; √3}
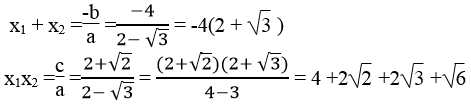
\(x^4+2x^2-3=0\Leftrightarrow x^4+3x^2-x^2-3=0\)
\(\Leftrightarrow x^2\left(x+3\right)-\left(x^2+3\right)=0\)
\(\Leftrightarrow\left(x^2+3\right)\left(x^2-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2=-3\left(vn\right)\\x^2=1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)
\(\Rightarrow-1+1=0\)