
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(10A=10.\dfrac{10^{2004}+1}{10^{2005}+1}=\dfrac{10^{2005}+10}{10^{2005}+1}=1+\dfrac{9}{10^{2005}+1}\\ 10B=10.\dfrac{10^{2005}+1}{10^{2006}+1}=\dfrac{10^{2006}+10}{10^{2006}+1}=1+\dfrac{9}{10^{2006}+1}\)
vì \(\dfrac{9}{10^{2005}+1}>\dfrac{9}{10^{2006}+1}\Rightarrow10A>10B\Rightarrow A>B\)

Giải:
A=102004+1/102005+1
10A=102005+10/102005+1
10A=102005+1+9/102005+1
10A=1+9/102005+1
Tương tự:
B=102005+1/102006+1
10B=1+9/102006+1
Vì 9/102005+1>9/102006+1 nên 10A>10B
⇒A>B
Chúc bạn học tốt!

Ta có: \(10\cdot A=\dfrac{10^{2005}+10}{10^{2005}+1}=1+\dfrac{9}{10^{2005}+1}\)
\(10B=\dfrac{10^{2006}+10}{10^{2006}+1}=1+\dfrac{9}{10^{2006}+1}\)
mà \(\dfrac{9}{10^{2005}+1}>\dfrac{9}{10^{2006}+1}\)
nên 10A>10B
hay A>B


Bài 4:
a chia 11 dư 5 dạng tổng quát của a là:
\(a=11k+5\left(k\in N\right)\)
b chia 11 dư 6 dạng tổng quát của b là:
\(b=11k+6\left(k\in N\right)\)
Nên: \(a+b\)
\(=11k+5+11k+6\)
\(=\left(11k+11k\right)+\left(5+6\right)\)
\(=k\cdot\left(11+11\right)+11\)
\(=22k+11\)
\(=11\cdot\left(2k+1\right)\)
Mà: \(11\cdot\left(2k+1\right)\) ⋮ 11
\(\Rightarrow a+b\) ⋮ 11
Bài 1: Mình làm rồi nhé !
Bài 2:
a) Dạng tổng quát của A là:
\(a=36k+24\left(k\in N\right)\)
b) a chia hết cho 6 vì:
Ta có: \(36k\) ⋮ 6 và 24 ⋮ 6
\(\Rightarrow a=36k+24\) ⋮ 6
c) a không chia hết cho 9 vì:
Ta có: \(36k\) ⋮ 9 và 24 không chia hết cho 9
\(\Rightarrow a=36k+24\) không chia hết cho 9

1 + 2 + 5 +1 = 9 chia hết cho 3 và 9.
5 + 3 + 1 + 6 = 15 chia hết cho 3 nhưng không chia hết cho 9.
Do đó:
1251 ⋮ 3 và 5316 ⋮ 3 ⇒ 1251 + 5316 ⋮ 3.
1251 ⋮ 9 và 5316 ⋮̸ 9 nên 1251 + 5316 ⋮̸ 9.

5 + 4 + 3 + 6 = 18 chia hết cho 3 và 9.
1 + 3 + 2 + 4 = 10 không chia hết cho cả 3 và 9.
Do đó:
5436 ⋮ 3 và 1324 ⋮̸ 3 nên 5436 – 1324 ⋮̸ 3.
5436 ⋮ 9 và 1324 ⋮̸ 9 nên 5436 – 1324 ⋮̸ 9.

Ta có: 1.2.3.4.5.6 chia hết cho 3.
1.2.3.4.5.6 = 1.2.4.5.(3.6) = 1.2.4.5.18 = 1.2.4.5.2.9 chia hết cho 9.
27 chia hết cho 3 và 9.
Do đó 1.2.3.4.5.6 + 27 chia hết cho 3 và 9.

1010 + 2 = 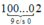
Tổng các chữ số bằng 1 + 0 + 0 + … + 0 + 2 = 3 chia hết cho 3 nhưng không chia hết cho 9
Do đó 1010 + 2 chia hết cho 3 nhưng không chia hết cho 9.

\(A=10^{37}-1\)
Mà: \(10^{37}=\overline{10...0}\) (37 số 0)
\(\Rightarrow A=10^{37}-1=\overline{10...0}-1=\overline{99...9}\)
Nên A chia hết cho 9 mà A chia hết cho 9 thì A chia hết cho 3
____________
\(A=10^{14}+2\)
Mà: \(10^{14}=\overline{10...0}\) (14 số 0)
\(\Rightarrow A=10^{14}+2=\overline{10...0}+2=\overline{10...2}\)
Tổng các chữ số là: 1 + 0 + ...+ 0 + 2 = 3
Nên A chia hết cho 3 không chia hết cho 9