
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b: Vì (d)//(d') nên a=3
Vậy: (d):y=3x+b
Thay x=4 và y=-5 vào (d), ta được:
b+12=-5
hay b=-17



trong \(\Delta ABH\) vuông tại H có
AH=AB.cosA=5.cos60=2,5
BH=\(\sqrt{AB^2-AH^2}\)(pytago)=\(\sqrt{5^2-2,5^2}\)=4,3
trong \(\Delta BHC\) vuông tại H có
\(HB^2=BC.BF\)(dl1)\(\Rightarrow BF=\dfrac{HB^2}{BC}\)=\(\dfrac{4,3^2}{5\sqrt{3}}\)=2,1
HF=\(\sqrt{HB^2-BF^2}\)=\(\sqrt{4,3^2-2,1^2}\)=3,8

Câu 9:
a) Ta có: \(9x^2-16=0\)
\(\Leftrightarrow\left(3x-4\right)\left(3x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{4}{3}\\x=-\dfrac{4}{3}\end{matrix}\right.\)
b) Ta có: \(4x^2=13\)
\(\Leftrightarrow x^2=\dfrac{13}{4}\)
\(\Leftrightarrow x\in\left\{\dfrac{\sqrt{13}}{2};-\dfrac{\sqrt{13}}{2}\right\}\)
c) Ta có: \(2x^2+9=0\)
\(\Leftrightarrow2x^2=-9\)(Vô lý)
d) Ta có: \(-x^2+324=0\)
\(\Leftrightarrow x^2=324\)
\(\Leftrightarrow\left[{}\begin{matrix}x=18\\x=-18\end{matrix}\right.\)



a: ĐKXĐ: x>0; x<>9
\(D=\dfrac{x+3+\sqrt{x}-3}{x-9}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}}\)
\(=\dfrac{x+\sqrt{x}}{\sqrt{x}}\cdot\dfrac{1}{\sqrt{x}+3}=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\)
b: x=2+căn 2-căn 2-1=1
Khi x=1 thì \(D=\dfrac{1+1}{1+3}=\dfrac{2}{4}=\dfrac{1}{2}\)
c: P=1:D=(căn x+3)/(căn x+1)
P nguyên
=>căn x+1+2 chia hết cho căn x+1
=>căn x+1 thuộc {1;2}
=>x=0(loại) hoặc x=1(nhận)
a) D có nghĩa khi: \(\left\{{}\begin{matrix}x\ge0\\x\ne9\end{matrix}\right.\)
\(D=\left(\dfrac{x+3}{x-9}-\dfrac{1}{\sqrt{x}+3}\right):\dfrac{\sqrt{x}}{\sqrt{x}-3}\)
\(D=\left(\dfrac{x+3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}-\dfrac{\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\right):\dfrac{\sqrt{x}}{\sqrt{x}-3}\)
\(D=\left(\dfrac{x+3+\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\right):\dfrac{\sqrt{x}}{\sqrt{x}-3}\)
\(D=\dfrac{\left(x+\sqrt{x}\right)\cdot\left(\sqrt{x}-3\right)}{\sqrt{x}\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(D=\dfrac{x+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+3\right)}=\dfrac{x+\sqrt{x}}{x+3\sqrt{x}}\)
\(D=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+3\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\)
b) \(x=\sqrt{6+4\sqrt{2}}-\sqrt{3+2\sqrt{2}}\)
\(x=\sqrt{2^2+2\cdot2\cdot\sqrt{2}+\left(\sqrt{2}\right)^2}-\sqrt{\left(\sqrt{2}\right)^2+2\cdot\sqrt{2}\cdot1+1^2}\)
\(x=\sqrt{\left(2+\sqrt{2}\right)^2}-\sqrt{\left(\sqrt{2}+1\right)^2}\)
\(x=\left|2+\sqrt{2}\right|-\left|\sqrt{2}+1\right|\)
\(x=2+\sqrt{2}-\sqrt{2}-1=1\)
Thay \(x=1\) vào D ta được:
\(D=\dfrac{\sqrt{1}+1}{\sqrt{1}+3}=\dfrac{2}{4}=\dfrac{1}{2}\)
c) Cho \(A=\dfrac{1}{D}=1:\left(\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\right)=\dfrac{\sqrt{x}+3}{\sqrt{x}+1}=\dfrac{\sqrt{x}+1+2}{\sqrt{x}+1}=\dfrac{\sqrt{x}+1}{\sqrt{x}+1}+\dfrac{2}{\sqrt{x}+1}=1+\dfrac{2}{\sqrt{x}+1}\)
A nguyên khi \(2⋮\sqrt{x}+1\)
\(\Rightarrow\sqrt{x}+1\inƯ\left(2\right)=\left\{1;2;-1;-2\right\}\)
Mà: \(\sqrt{x}>0\)
\(\Rightarrow\sqrt{x}+1\in\left\{1;2\right\}\)
\(\Rightarrow\left\{{}\begin{matrix}x=0\left(ktm\right)\\x=1\left(tm\right)\end{matrix}\right.\)

để em viết ra vậy ạ
cho tam giac mnp vuông tại m (mn>mp) có đường cao mk
a) biết mn=20cm, mp=15cm, tính mk và góc mnp (góc làm tròn đến đơn vị phút).
b) vẽ trung tuyến me của tam giác mnp. từ p vẽ đường thẳng vuông góc với me cắt mn tại d. cm tam giác mnp đồng dạng với tam giác mpd, từ đó suy ra mn.md=np.pk



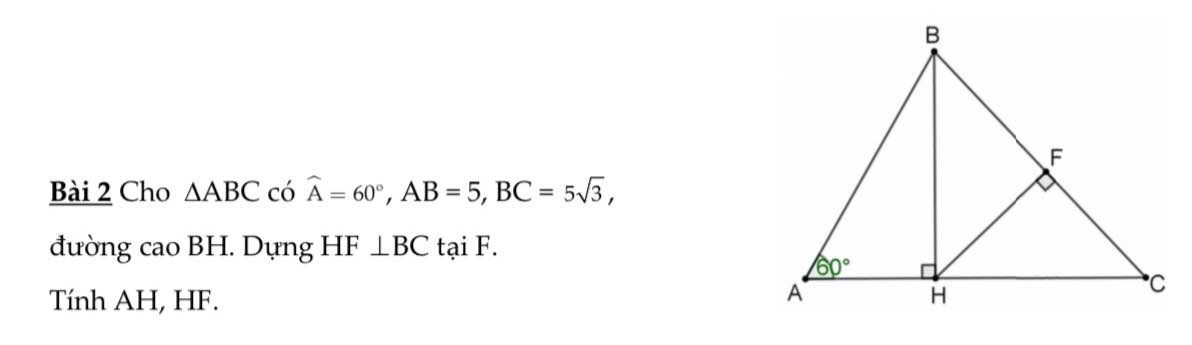
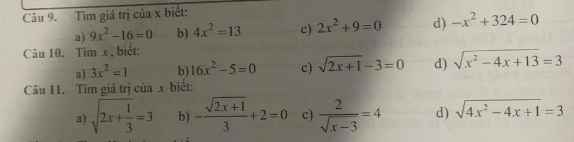


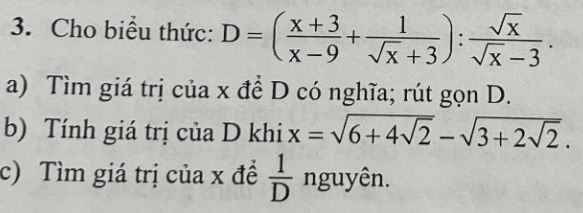
a,tam giác bmh vuông tại h có đường cao mh nên ah^2=am.ab
tương tự ah^2=ac.an
suy ra đpcm
b,chứng minh dc \(\Delta AMN\sim\Delta ACB\left(g.g\right)\\\)
suy ra \(\dfrac{S_{AMN}}{S_{ABC}}=\dfrac{MN^2}{BC^2}=\dfrac{AH^2}{BC^2}=\dfrac{AH^4}{\left(AH.BC\right)^2}=\dfrac{AH^4}{\left(2S\right)^2}\\ =\dfrac{AH^4}{\left(AB.AC\right)^2}=\dfrac{AH^2}{AB^2}.\dfrac{AH^2}{AC^2}=sin^2B.sin^2C\left(đpcm\right)\)
tick mik nha
bạn có nhầm ko? 2 tam giác này có chung góc A mà bạn
hoặc là 2 tam giác này đều có góc A=90