
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 9:
a) Ta có: \(9x^2-16=0\)
\(\Leftrightarrow\left(3x-4\right)\left(3x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{4}{3}\\x=-\dfrac{4}{3}\end{matrix}\right.\)
b) Ta có: \(4x^2=13\)
\(\Leftrightarrow x^2=\dfrac{13}{4}\)
\(\Leftrightarrow x\in\left\{\dfrac{\sqrt{13}}{2};-\dfrac{\sqrt{13}}{2}\right\}\)
c) Ta có: \(2x^2+9=0\)
\(\Leftrightarrow2x^2=-9\)(Vô lý)
d) Ta có: \(-x^2+324=0\)
\(\Leftrightarrow x^2=324\)
\(\Leftrightarrow\left[{}\begin{matrix}x=18\\x=-18\end{matrix}\right.\)


`a)m=0=>x^2-x+3=0<=>(x-1/2)^2+11/4=0` (Vô lí)
`=>m=0` ptr vô nghiệm
`b)` Ptr có nghiệm kép `<=>\Delta=0`
`<=>[-(2m+1)]^2-4(m^2+3)=0`
`<=>4m^2+4m+1-4m^2-12=0`
`<=>4m-11=0`
`<=>m=11/4`
`c)` Ptr có `2` nghiệm pb`<=>\Delta > 0`
`<=>4m-11 > 0<=>m > 11/4`
`d)` Ptr vô nghiệm `<=>\Delta < 0<=>4m-11 < 0<=>m < 11/4`
Bài 2:
a: Khi m=0 thì pt sẽ là:
\(x^2-x+3=0\)
=>\(x\in\varnothing\)
b: \(\Delta=\left(2m+1\right)^2-4\left(m^2+3\right)\)
=4m^2+4m+1-4m^2-12
=4m-11
Để pt có nghiệm kép thì 4m-11=0
=>m=11/4
c: Để phương trình có hai nghiệm pb thì 4m-11>0
=>m>11/4
d: Để pt vô nghiệm thì 4m-11<0
=>m<11/4

a: ΔOBC cân tại O
ma OI là trung tuyến
nên OI vuông góc BC
=>góc OIA=90 độ
góc OIA=góc OMA=góc ONA=90 độ
=>O,I,M,A,N cùng thuộc đường tròn đường kính OA
Tâm là trung điểm của OA
R'=OA/2=R
b: Xét ΔAON vuông tại N có cos AON=ON/OA=1/2
nêngóc AON=60 độ
=>góc MON=120 độ
sđ cung MN=120 độ
c: Xét ΔAMB và ΔACM có
góc AMB=góc ACM
góc MAB chung
=>ΔAMB đồng dạng với ΔACM
=>AM/AC=AB/AM
=>AM^2=AB*AC

a: Ta có: \(\left(12-6\sqrt{3}\right)\cdot\sqrt{\dfrac{3}{14-8\sqrt{3}}}-3\cdot\sqrt{2\left(1-\sqrt{1-\sqrt{4-2\sqrt{3}}}\right)+2\sqrt{4+2\sqrt{3}}}\)
\(=\left(3-\sqrt{3}\right)\cdot\dfrac{\sqrt{3}}{2\sqrt{2}-\sqrt{6}}-3\cdot\sqrt{2\cdot\left(1-\sqrt{1-\sqrt{3}+1}\right)+2\cdot\left(\sqrt{3}+1\right)}\)
\(=\left(3-\sqrt{3}\right)\cdot\dfrac{\sqrt{6}\left(2+\sqrt{3}\right)}{2}-3\cdot\sqrt{\left(2-\sqrt{2}\cdot\sqrt{4-2\sqrt{3}}\right)+2\sqrt{3}+2}\)
\(=\dfrac{\left(3\sqrt{6}-3\sqrt{2}\right)\left(2+\sqrt{3}\right)}{2}-3\cdot\sqrt{2-\sqrt{2}\left(\sqrt{3}+1\right)+2\sqrt{3}+2}\)
\(=\dfrac{3\sqrt{6}+3\sqrt{2}}{2}-3\cdot\sqrt{2-\sqrt{6}-\sqrt{2}+2\sqrt{3}+2}\)
Đến đây thì xin lỗi bạn, mình thua
b: Ta có: \(x^4+6x^3+11x^2+6x+1\)
\(=x^4+3x^3+x^2+3x^3+9x^2+3x+x^2+3x+1\)
\(=\left(x^2+3x+1\right)^2\) là số chính phương(đpcm)



Bài 2:
b: 2x-4y=5
=>4y=2x+5
=>y=1/2x+5/4
Vậy: Hệ số góc là 1/2
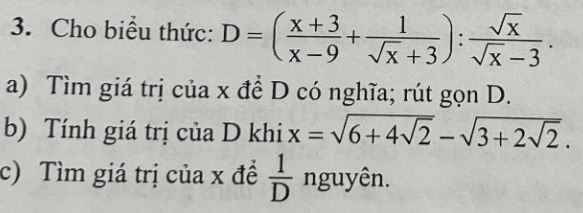
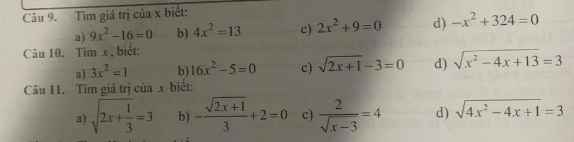

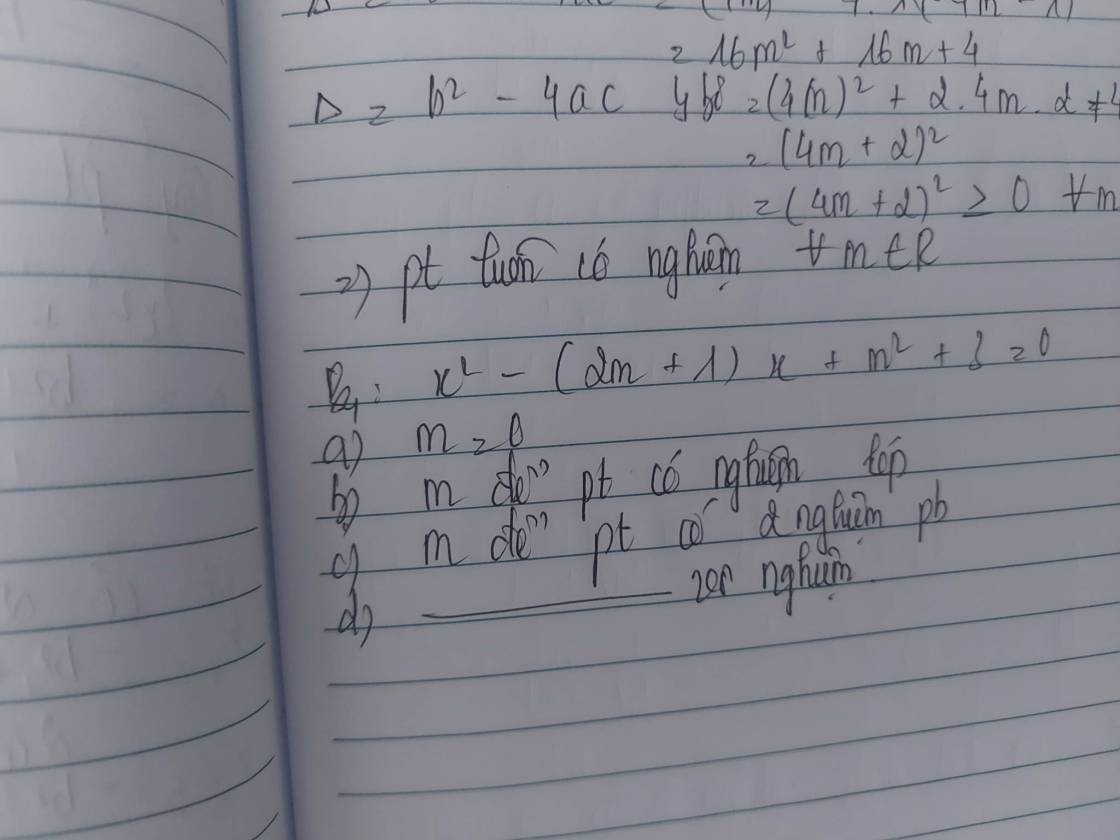


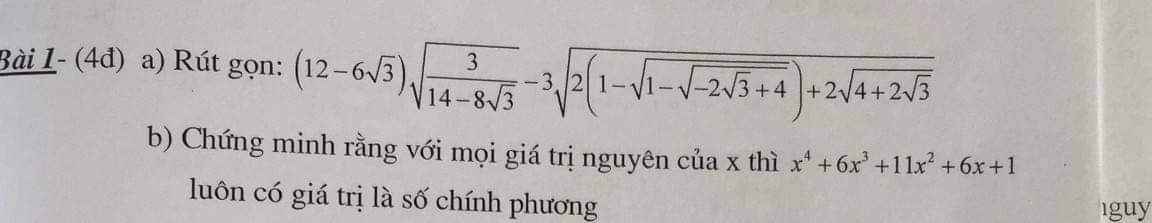


a: ĐKXĐ: x>0; x<>9
\(D=\dfrac{x+3+\sqrt{x}-3}{x-9}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}}\)
\(=\dfrac{x+\sqrt{x}}{\sqrt{x}}\cdot\dfrac{1}{\sqrt{x}+3}=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\)
b: x=2+căn 2-căn 2-1=1
Khi x=1 thì \(D=\dfrac{1+1}{1+3}=\dfrac{2}{4}=\dfrac{1}{2}\)
c: P=1:D=(căn x+3)/(căn x+1)
P nguyên
=>căn x+1+2 chia hết cho căn x+1
=>căn x+1 thuộc {1;2}
=>x=0(loại) hoặc x=1(nhận)
a) D có nghĩa khi: \(\left\{{}\begin{matrix}x\ge0\\x\ne9\end{matrix}\right.\)
\(D=\left(\dfrac{x+3}{x-9}-\dfrac{1}{\sqrt{x}+3}\right):\dfrac{\sqrt{x}}{\sqrt{x}-3}\)
\(D=\left(\dfrac{x+3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}-\dfrac{\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\right):\dfrac{\sqrt{x}}{\sqrt{x}-3}\)
\(D=\left(\dfrac{x+3+\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\right):\dfrac{\sqrt{x}}{\sqrt{x}-3}\)
\(D=\dfrac{\left(x+\sqrt{x}\right)\cdot\left(\sqrt{x}-3\right)}{\sqrt{x}\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(D=\dfrac{x+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+3\right)}=\dfrac{x+\sqrt{x}}{x+3\sqrt{x}}\)
\(D=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+3\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\)
b) \(x=\sqrt{6+4\sqrt{2}}-\sqrt{3+2\sqrt{2}}\)
\(x=\sqrt{2^2+2\cdot2\cdot\sqrt{2}+\left(\sqrt{2}\right)^2}-\sqrt{\left(\sqrt{2}\right)^2+2\cdot\sqrt{2}\cdot1+1^2}\)
\(x=\sqrt{\left(2+\sqrt{2}\right)^2}-\sqrt{\left(\sqrt{2}+1\right)^2}\)
\(x=\left|2+\sqrt{2}\right|-\left|\sqrt{2}+1\right|\)
\(x=2+\sqrt{2}-\sqrt{2}-1=1\)
Thay \(x=1\) vào D ta được:
\(D=\dfrac{\sqrt{1}+1}{\sqrt{1}+3}=\dfrac{2}{4}=\dfrac{1}{2}\)
c) Cho \(A=\dfrac{1}{D}=1:\left(\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\right)=\dfrac{\sqrt{x}+3}{\sqrt{x}+1}=\dfrac{\sqrt{x}+1+2}{\sqrt{x}+1}=\dfrac{\sqrt{x}+1}{\sqrt{x}+1}+\dfrac{2}{\sqrt{x}+1}=1+\dfrac{2}{\sqrt{x}+1}\)
A nguyên khi \(2⋮\sqrt{x}+1\)
\(\Rightarrow\sqrt{x}+1\inƯ\left(2\right)=\left\{1;2;-1;-2\right\}\)
Mà: \(\sqrt{x}>0\)
\(\Rightarrow\sqrt{x}+1\in\left\{1;2\right\}\)
\(\Rightarrow\left\{{}\begin{matrix}x=0\left(ktm\right)\\x=1\left(tm\right)\end{matrix}\right.\)