Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(1,=2\sqrt{3}-3\sqrt{3}+4\sqrt{3}=3\sqrt{3}\\ 2,=\left(2\sqrt{6}+2\sqrt{5}-4\sqrt{5}\right):5=\dfrac{2\sqrt{6}}{5}-\dfrac{2\sqrt{5}}{5}\\ 3,=6\sqrt{3}-\dfrac{4\sqrt{3}}{3}-4\sqrt{3}-\dfrac{5\sqrt{3}}{3}=2\sqrt{3}-\dfrac{9\sqrt{3}}{3}=2\sqrt{3}-3\sqrt{3}=-\sqrt{3}\\ 4,Sửa:\dfrac{1}{\sqrt{5}-\sqrt{3}}-\dfrac{1}{\sqrt{5}+\sqrt{3}}\\ =\dfrac{\sqrt{5}+\sqrt{3}-\sqrt{5}+\sqrt{3}}{\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}+\sqrt{3}\right)}=\dfrac{2\sqrt{3}}{2}=\sqrt{3}\)
1) \(=2\sqrt{3}-3\sqrt{3}+4\sqrt{3}=3\sqrt{3}\)
2) \(=\left(2\sqrt{6}+2\sqrt{5}-4\sqrt{5}\right)=\dfrac{2\sqrt{6}}{5}+\dfrac{2\sqrt{5}}{5}-\dfrac{4\sqrt{5}}{5}\)
3) \(=6\sqrt{3}-\dfrac{4\sqrt{3}}{3}-4\sqrt{3}-\dfrac{5\sqrt{3}}{3}=2\sqrt{3}-3\sqrt{3}=-\sqrt{3}\)
4) \(=\dfrac{\sqrt{5}+\sqrt{3}-\sqrt{5}+\sqrt{3}}{5-3}=\dfrac{2\sqrt{3}}{2}=\sqrt{3}\)

a: \(5\sqrt{2}-8\sqrt{3}+30\sqrt{3}-6\sqrt{3}=5\sqrt{2}+16\sqrt{3}\)
b: \(=14\sqrt{3}-\dfrac{3}{32}\cdot8\sqrt{3}+\dfrac{4}{18}\cdot9\sqrt{3}-\dfrac{1}{10}\cdot10\sqrt{3}\)
\(=14\sqrt{3}-\dfrac{3}{4}\sqrt{3}+2\sqrt{3}-1\sqrt{3}=\dfrac{57}{4}\sqrt{3}\)
c: \(=\dfrac{-1}{2}\cdot6\sqrt{3}+\dfrac{1}{15}\cdot5\sqrt{3}-\dfrac{1}{22}\cdot11\sqrt{3}+2\sqrt{3}\)
\(=-3\sqrt{3}+\dfrac{1}{3}\sqrt{3}-\dfrac{1}{2}\sqrt{3}+2\sqrt{3}=-\dfrac{7}{6}\sqrt{3}\)
d: \(=\dfrac{5}{8}\cdot4\sqrt{3}-\dfrac{1}{33}\cdot11\sqrt{3}+\dfrac{3}{14}\cdot7\sqrt{3}-\dfrac{1}{4}\cdot8\sqrt{3}\)
\(=\dfrac{5}{2}\sqrt{3}-\dfrac{1}{3}\sqrt{3}+\dfrac{3}{2}\sqrt{3}-2\sqrt{3}=\dfrac{5}{3}\sqrt{3}\)

a: =(2căn 3-8căn 3)(căn 3-1)
=-6căn 3*(căn 3-1)
=-18+6căn 3
b: \(=\dfrac{6-2\sqrt{5}}{\sqrt{5}-3}-\sqrt{5}+2\)
=-2-căn 5+2=-căn 5
c: \(=3\sqrt{2a}-3a\sqrt{2a}+2\sqrt{2a}-\dfrac{1}{4}\cdot8\sqrt{2a}\)
=\(3\sqrt{2a}-3a\cdot\sqrt{2a}\)

a) Ta có: \(\dfrac{2\sqrt{8}-\sqrt{12}}{\sqrt{18}-\sqrt{48}}-\dfrac{\sqrt{5}+\sqrt{27}}{\sqrt{30}+\sqrt{162}}\)
\(=\dfrac{-2\left(\sqrt{3}-\sqrt{8}\right)}{\sqrt{6}\left(\sqrt{3}-\sqrt{6}\right)}-\dfrac{\sqrt{5}+\sqrt{27}}{\sqrt{6}\left(\sqrt{5}+\sqrt{27}\right)}\)
\(=\dfrac{-3}{\sqrt{6}}=\dfrac{-3\sqrt{6}}{6}=\dfrac{-\sqrt{6}}{2}\)
b) Ta có: \(\left(1+\sqrt{2}+\sqrt{3}\right)\left(1-\sqrt{2}-\sqrt{3}\right)\)
\(=1-\left(\sqrt{2}+\sqrt{3}\right)^2\)
\(=1-5-2\sqrt{6}\)
\(=-4-2\sqrt{6}\)

Bài 1:
a) Ta có: \(\left(5\sqrt{\dfrac{1}{5}}+\dfrac{1}{2}\sqrt{20}-\dfrac{5}{4}\sqrt{\dfrac{4}{5}}+\sqrt{5}\right)\)
\(=\left(\sqrt{5}+\sqrt{5}-\dfrac{5}{4}\cdot\dfrac{2}{\sqrt{5}}+\sqrt{5}\right)\)
\(=3\sqrt{5}-\dfrac{1}{2}\sqrt{5}\)
\(=\dfrac{5}{2}\sqrt{5}\)
c) Ta có: \(\dfrac{5\sqrt{7}-7\sqrt{5}+2\sqrt{70}}{\sqrt{35}}\)
\(=\dfrac{\sqrt{35}\left(\sqrt{5}-\sqrt{7}+2\sqrt{2}\right)}{\sqrt{35}}\)
\(=2\sqrt{2}+\sqrt{5}-\sqrt{7}\)
Bài 2:
e) ĐKXĐ: \(\dfrac{4}{3}\le x\le6\)
Ta có: \(\sqrt{6-x}=3x-4\)
\(\Leftrightarrow6-x=\left(3x-4\right)^2\)
\(\Leftrightarrow9x^2-24x+16+6-x=0\)
\(\Leftrightarrow9x^2-25x+22=0\)
\(\Delta=\left(-25\right)^2-4\cdot9\cdot22=625-792< 0\)
Vậy: Phương trình vô nghiệm

\(A=\sqrt{243}-\sqrt{27}+\sqrt{3}-\sqrt{48}\\ =\sqrt{81\cdot3}-\sqrt{9\cdot3}+\sqrt{3}-\sqrt{16\cdot3}\\ =9\sqrt{3}-3\sqrt{3}+\sqrt{3}-4\sqrt{4}\\ =\left(9-3+1-4\right)\sqrt{3}\\ =3\sqrt{3}\)
\(B=\dfrac{5+\sqrt{5}}{\sqrt{5}}+\dfrac{3+\sqrt{3}}{\sqrt{3}+1}-\left(\sqrt{3}+\sqrt{5}\right)\\ =\dfrac{\sqrt{5}\left(\sqrt{5}+1\right)}{\sqrt{5}}+\dfrac{\sqrt{3}\left(\sqrt{3}+1\right)}{\sqrt{3}+1}-\sqrt{5}-\sqrt{3}\\ =\sqrt{5}+1+\sqrt{3}-\sqrt{5}-\sqrt{3}\\ =1\)

Bài 1:
a: \(5\sqrt{8}-4\sqrt{27}-2\sqrt{75}+\sqrt{108}\)
\(=5\cdot2\sqrt{2}-4\cdot3\sqrt{3}-2\cdot5\sqrt{3}+6\sqrt{3}\)
\(=10\sqrt{2}-12\sqrt{3}-10\sqrt{3}+6\sqrt{3}\)
\(=10\sqrt{2}-16\sqrt{3}\)
b: \(\sqrt{\left(3-\sqrt{6}\right)^2}+\sqrt{\left(1-\sqrt{6}\right)^2}\)
\(=\left|3-\sqrt{6}\right|+\left|1-\sqrt{6}\right|\)
\(=3-\sqrt{6}+\sqrt{6}-1\)
=3-1=2
c: \(\dfrac{5\sqrt{3}-3\sqrt{5}}{\sqrt{5}-\sqrt{3}}+\dfrac{1}{4+\sqrt{15}}\)
\(=\dfrac{\sqrt{15}\left(\sqrt{5}-\sqrt{3}\right)}{\sqrt{5}-\sqrt{3}}+\dfrac{1\left(4-\sqrt{15}\right)}{16-15}\)
\(=\sqrt{15}+4-\sqrt{15}=4\)
d: \(\dfrac{2\sqrt{3-\sqrt{5}}\cdot\left(3+\sqrt{5}\right)}{\sqrt{10}-\sqrt{2}}-\dfrac{\sqrt{15}+\sqrt{5}}{\sqrt{12}+2}\)
\(=\dfrac{\sqrt{3-\sqrt{5}}\cdot\sqrt{2}\left(3+\sqrt{5}\right)}{\sqrt{5}-1}-\dfrac{\sqrt{5}\left(\sqrt{3}+1\right)}{2\left(\sqrt{3}+1\right)}\)
\(=\dfrac{\sqrt{6-2\sqrt{5}}\cdot\left(3+\sqrt{5}\right)}{\sqrt{5}-1}-\dfrac{\sqrt{5}}{2}\)
\(=\sqrt{\left(\sqrt{5}-1\right)^2}\cdot\dfrac{\left(3+\sqrt{5}\right)}{\sqrt{5}-1}-\dfrac{\sqrt{5}}{2}\)
\(=3+\sqrt{5}-\dfrac{\sqrt{5}}{2}=3+\dfrac{\sqrt{5}}{2}\)
Bài 2:
Vẽ đồ thị:
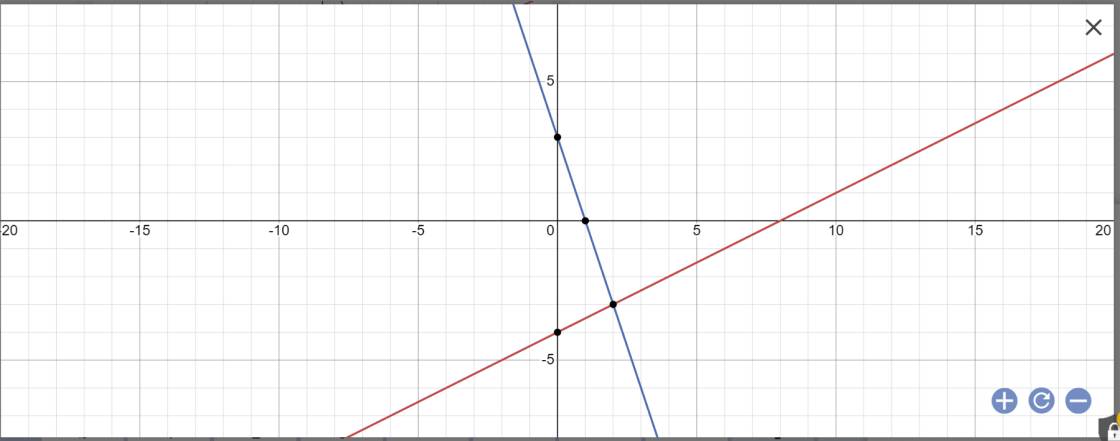
Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x-4=-3x+3\)
=>\(\dfrac{1}{2}x+3x=3+4\)
=>\(\dfrac{7}{2}x=7\)
=>x=2
Thay x=2 vào y=-3x+3, ta được:
\(y=-3\cdot2+3=-3\)
Vậy: (d1) cắt (d2) tại A(2;-3)

A: \(A=\sqrt{9}-3\sqrt{\dfrac{50}{9}}+3\sqrt{8}-\sqrt[3]{27}\)
\(=3-3\cdot\dfrac{5\sqrt{2}}{3}+6\sqrt{2}-3\)
\(=-5\sqrt{2}+6\sqrt{2}=\sqrt{2}\)
b: \(B=\sqrt{\left(2-\sqrt{3}\right)^2}+\dfrac{2}{\sqrt{3}-1}-6\cdot\sqrt{\dfrac{16}{3}}\)
\(=\left|2-\sqrt{3}\right|+\dfrac{2\left(\sqrt{3}+1\right)}{3-1}-6\cdot\dfrac{4}{\sqrt{3}}\)
\(=2-\sqrt{3}+\sqrt{3}+1-4\sqrt{3}\)
\(=3-4\sqrt{3}\)
\(A=\sqrt{9}-3\sqrt{\dfrac{50}{9}}+3\sqrt{8}-\sqrt[3]{27}\\ =3-3\cdot\dfrac{1}{3}\sqrt{25\cdot2}+3\sqrt{4\cdot2}-3\\ =3-1\cdot5\sqrt{2}+3\cdot2\sqrt{2}-3\\ =3-5\sqrt{2}+6\sqrt{2}-3\\ =\sqrt{2}\)
\(B=\sqrt{\left(2-\sqrt{3}\right)^2}+\dfrac{2}{\sqrt{3}-1}-6\sqrt{\dfrac{16}{3}}\\ =\left|2-\sqrt{3}\right|+\dfrac{2\left(\sqrt{3}+1\right)}{3-1}-6\cdot\dfrac{4\sqrt{3}}{3}\\ =2-\sqrt{3}+\sqrt{3}+1-8\sqrt{3}\\ =3-8\sqrt{3}\)
a) Ta có: \(-3\sqrt{16}\cdot\sqrt{90}\)
\(=-3\cdot4\cdot3\sqrt{10}\)
\(=-36\sqrt{10}\)
b) Ta có: \(3\sqrt{\dfrac{4}{3}}-3\sqrt{48}+5\sqrt{75}\)
\(=3\cdot\dfrac{2}{\sqrt{3}}-3\cdot4\sqrt{3}+5\cdot5\sqrt{3}\)
\(=2\sqrt{3}-12\sqrt{3}+25\sqrt{3}\)
\(=15\sqrt{3}\)
c) Ta có: \(4\sqrt[3]{27}-\sqrt[3]{64}-2\sqrt[3]{8}\)
\(=4\cdot3-4-2\cdot2\)
\(=12-4-4=4\)