
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NH
1

Các câu hỏi dưới đây có thể giống với câu hỏi trên

26 tháng 10 2017
\(S=\frac{1}{2}.\frac{3}{5}.\frac{5}{7}...\frac{2015}{2017}\)
\(=\frac{1}{2017}\)
Cách phân tích thì dễ thôi\(\frac{1}{2^2-1}=\frac{1}{\left(2-1\right)\left(2+1\right)}=\frac{1}{3}\)
Các cái kia tương tự
26 tháng 10 2017
\(S=\frac{1}{3}.\frac{3}{5}.\frac{5}{7}...\frac{2015}{2017}\)
Mình ghi nhầm
RW
0

TY
0

LQ
2

2 tháng 9 2021
\(A=-1^2+2^2-3^2+4^2-5^2+6^2-...-2015^2+2016^2\)
\(=1+2+3+...+2016\)
\(=2017\cdot1008=2033136\)
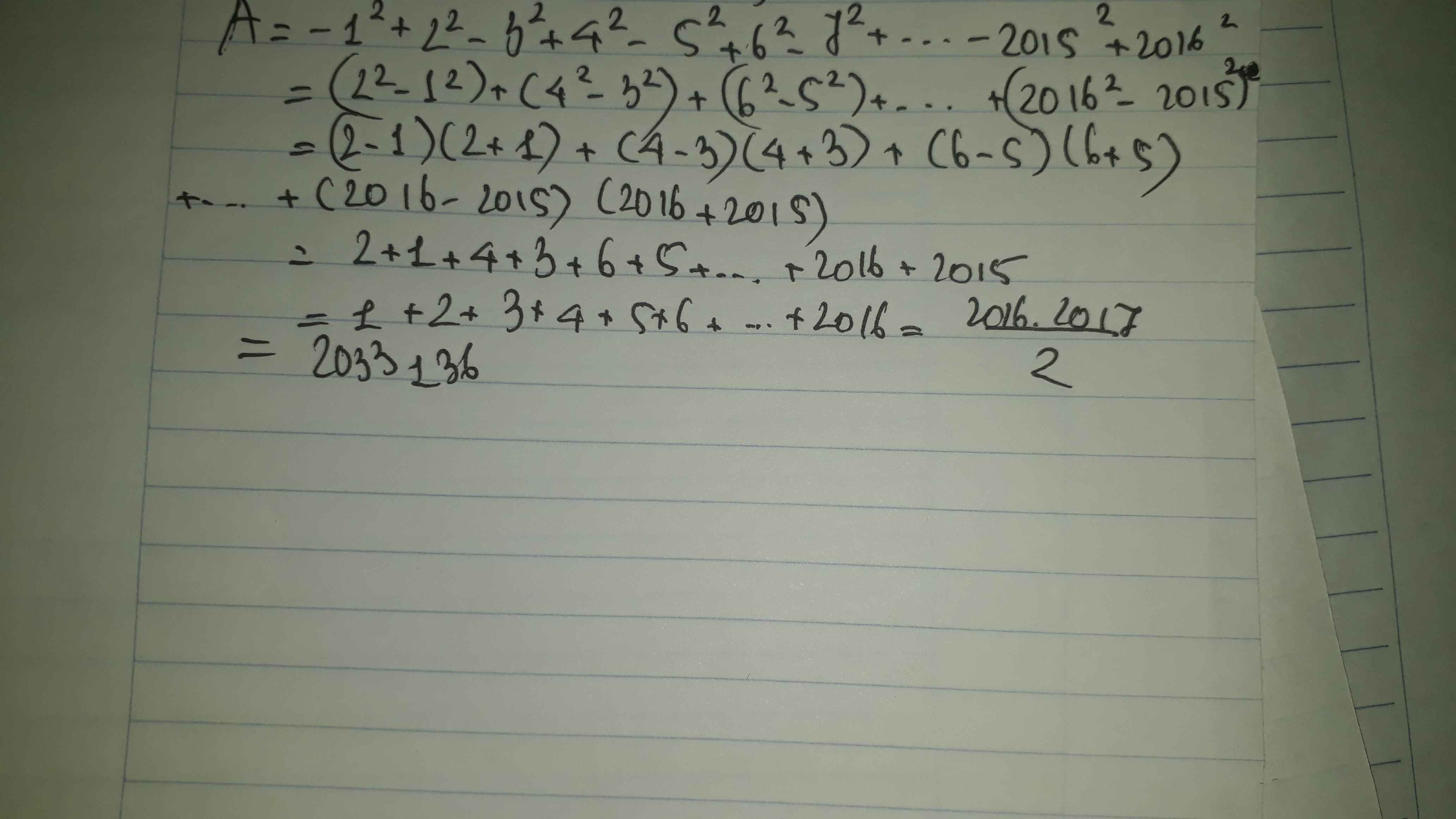
Ta có : A= x^0+ x^1+ x^2+...+x^n => \(A=\frac{x^{n+1}-1}{x-1}\)
Chứng minh: xA=x1+x2+...+x^n+1
xA-A=A(x-1)=xn+1-x0=xn+1-1
Từ đó => điều trên
Vậy Ta có:
\(S=\frac{\left(-\frac{1}{7}\right)^{2017}-1}{-\frac{1}{7}-1}\)