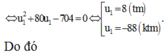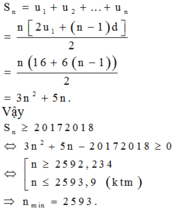K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
30 tháng 11 2023
1.
Trước hết bạn nhớ công thức:
$1^2+2^2+....+n^2=\frac{n(n+1)(2n+1)}{6}$ (cách cm ở đây: https://hoc24.vn/cau-hoi/tinh-tongs-122232n2.83618073020)
Áp vào bài:
\(\lim\frac{1}{n^3}[1^2+2^2+....+(n-1)^2]=\lim \frac{1}{n^3}.\frac{(n-1)n(2n-1)}{6}=\lim \frac{n(n-1)(2n-1)}{6n^3}\)
\(=\lim \frac{(n-1)(2n-1)}{6n^2}=\lim (\frac{n-1}{n}.\frac{2n-1}{6n})=\lim (1-\frac{1}{n})(\frac{1}{3}-\frac{1}{6n})\)
\(=1.\frac{1}{3}=\frac{1}{3}\)
AH
Akai Haruma
Giáo viên
30 tháng 11 2023
2.
\(\lim \frac{1}{n}\left[(x+\frac{a}{n})+(x+\frac{2a}{n})+...+(x.\frac{(n-1)a}{n}\right]\)
\(=\lim \frac{1}{n}\left[\underbrace{(x+x+...+x)}_{n-1}+\frac{a(1+2+...+n-1)}{n} \right]\)
\(=\lim \frac{1}{n}[(n-1)x+a(n-1)]=\lim \frac{n-1}{n}(x+a)=\lim (1-\frac{1}{n})(x+a)\)
\(=x+a\)
TM
1
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 10 2021
Đề là \(\dfrac{cos^2x}{3}+\dfrac{sinx}{3}+1\) hay \(cos^2\left(\dfrac{x}{3}\right)+sin\left(\dfrac{x}{3}\right)+1\) vậy nhỉ?
CM
19 tháng 1 2019
Chọn A
Với số tự nhiên n ≥ 1, ta có:
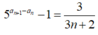
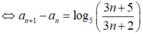
Suy ra:
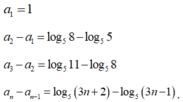
Cộng tương ứng hai vế các đẳng thức trên ta có 
với mọi số tự nhiên n
≥
1
Để 
Ta kiểm tra với các giá trị k ∈ ℕ từ bé đến lớn
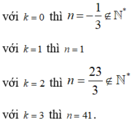
Vậy số nguyên n > 1 nhỏ nhất là n = 41( ứng với k = 3).
DD
7
14 tháng 12 2021
\(21+22+23+...+n+4840\)
\(\Rightarrow\left[\left(n-21\right):1+1\right]\left(n+21\right):2=4840\)
\(\Rightarrow\left(n-20\right)\left(n+21\right)=9680\)
\(\Rightarrow n^2+n-420=9680\)
\(\Leftrightarrow n^2+n-100100=0\)
\(\Leftrightarrow n^2-100n+101n-100100=0\)
\(\Leftrightarrow n\left(n-100\right)+101\left(n-100\right)=0\)
\(\Leftrightarrow\left(n+101\right)\left(n-100\right)=0\)
\(\Leftrightarrow\left[n=-101\text{(loại)},n=100\right]\)
\(\Rightarrow n=100\)
\(\text{Hok tốt!}\)
\(\text{@Kaito Kid}\)
XO
26 tháng 11 2021
21 + 22 + 23 + ... + n = 4840
=> [(n - 21) : 1 + 1](n + 21) : 2 = 4840
=> (n - 20)(n + 21) = 9680
=> n2 + n - 420 = 9680
<=> n2 + n - 10100 = 0
<=> n2 - 100n + 101n - 10100 = 0
<=> n(n - 100) + 101(n - 100) = 0
<=> (n + 101)(n - 100) = 0
<=> \(\orbr{\begin{cases}n=-101\left(\text{loại}\right)\\n=100\end{cases}}\)
Vậy n = 100