Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta có khái niệm : Tia phân giác của 2 góc kề bù tao thành 1 góc có tổng số đo la 90 độ
nên om vuông góc với on

góc xOy = xOz - yOz
vì xOy và yOz là 2 góc kề bù nên có tổn là 180*
Nên
xOy = xOz - yOz
xOy = 180 - 64
xOy = 116
góc mOy = mOx = xOy : 2 (vì Om là tia phân giác của góc xOy)
=> mOy = mOx = 116 : 2 = 58
góc yOn = nOz = yOz : 2 (vì On là tia phân giác của góc yOz)
=> yOn = nOz = 64 : 2 = 32
chứng minh Om vuông góc On
ta có :
mOy + yOn = mOn
58 + 32 = 90
=> Om vuông góc On

Vì góc yOz và góc xOy là hai góc kề bù nên Oz và Ox cùng nằm trên một đường thẳng zx (1)
Tương tự ta có: Ot và Oy cùng nằm trên một đường thẳng
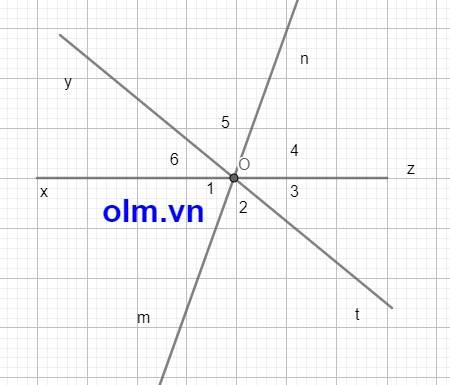
\(\widehat{xOt}\) và \(\widehat{yOz}\) là hai góc đối đỉnh
⇒ \(\widehat{O_2}\) = \(\dfrac{1}{2}\) \(\widehat{xOt}\) = \(\dfrac{1}{2}\) \(\widehat{yOz}\) = \(\widehat{O_5}\)
Mặt khác ta có: \(\widehat{O_2}\) + \(\widehat{O_1}\) + \(\widehat{O_6}\) = 1800 (gt)
⇒ \(\widehat{O_1}\) + \(\widehat{O_6}\) + \(\widehat{O_5}\) = 1800
⇒ Om và On cùng thuộc một đường thẳng mn (2)
Kết hợp (1) và (2) ta có: góc zOn và góc xOm là hai góc đối đỉnh