K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
11 tháng 1 2017
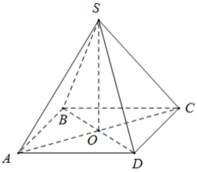
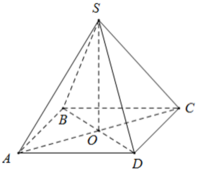
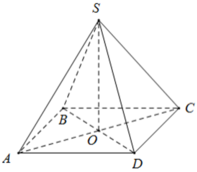
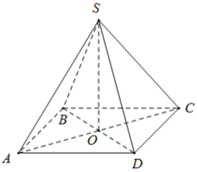
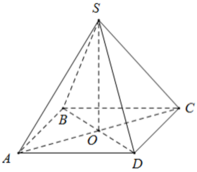
Ta có ABCD là hình vuông, khi đó nửa chu vi bằng:
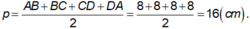
+ BD = AC = √ (82 + 82) = 8√ 2 ( cm ) ⇒ AO = BO = CO = DO = 4√ 2 ( cm )
Do đó:
+ Diện tích xung quanh của hình chóp đều là Sxq = p.d = p.OB = 16.4√ 2 = 64√ 2 ( cm2 ).
+ Diện tích toàn phần của hình chóp đều là
Stp = Sxq + SABCD = 64√ 2 + 82 = 64 + 64√ 2 ( cm2 )
+ Thể tích của hình chóp đều là V = 1/3S.h = 1/3.SABCD.SO = 1/3.82.10 = 640/3( cm3 )

H9
HT.Phong (9A5)
CTVHS
10 tháng 10 2023
Diện tích đáy của hình chóp tứ giá đều:
\(V=\dfrac{1}{3}Sh\Rightarrow S=\dfrac{3V}{h}=\dfrac{3\cdot13,5}{4,5}=9\left(cm^2\right)\)
Độ dài cạnh đáy là:
\(\sqrt{9}=3\left(cm\right)\)
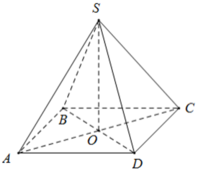
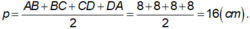

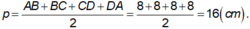

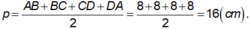

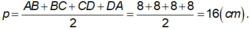

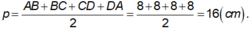

`#3107.101107`
Hình chóp là tam giác đều hay tứ giác đều nhỉ? Mình làm mẫu 1 cái nhé
Diện tích của mặt đáy hình chóp tứ giác (tam giác) đều:
\(\text{S}_{\text{xq}}=a^2=10^2=100\left(\text{cm}^2\right)\)
(\(\text{S}_{\text{xq}}=\dfrac{1}{2}\cdot a\cdot h=\dfrac{1}{2}\cdot5\cdot10=25\left(\text{cm}^2\right)\))
Thể tích của hình chóp tứ giác (tam giác) đều:
\(\text{V}_{\text{hình chóp}}=\dfrac{1}{3}\cdot s\cdot h=\dfrac{1}{3}\cdot100\cdot5\approx166,7\left(\text{cm}^3\right)\)
(\(\text{V}_{\text{hình chóp}}=\dfrac{1}{3}\cdot s\cdot h=\dfrac{1}{3}\cdot25\cdot10\approx83,3\left(\text{cm}^3\right).\))