K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 11 2021
Gọi H là hình chiếu vuông góc của A' lên (ABCD)
Do \(A'A=A'B=A'D\) \(\Rightarrow H\) trùng tâm đường tròn ngoại tiếp tam giác ABD
\(\Rightarrow H\) là trung điểm BD
\(AC=\sqrt{AB^2+AD^2}=2a\)\(\Rightarrow AH=\dfrac{1}{2}AC=a\)
\(\Rightarrow A'H=\sqrt{A'A^2-AH^2}=a\sqrt{3}\)
\(\Rightarrow V=A'H.AB.AD=3a^3\)

20 tháng 10 2021
\(AA'=\dfrac{2a}{\sqrt{3}}\)
\(V=AA'\cdot S_{ABCD}=\dfrac{16a^3}{\sqrt{3}}\)

NV
Nguyễn Việt Lâm
Giáo viên
31 tháng 8 2021
\(AC=AB\sqrt{2}=4a\)
Áp dụng định lý Pitago:
\(CC'=\sqrt{\left(AC'\right)^2-AC^2}=3a\)
\(\Rightarrow V=3a.\left(2a\sqrt{2}\right)^2=24a^3\)
LL
0

NH
1

18 tháng 12 2023
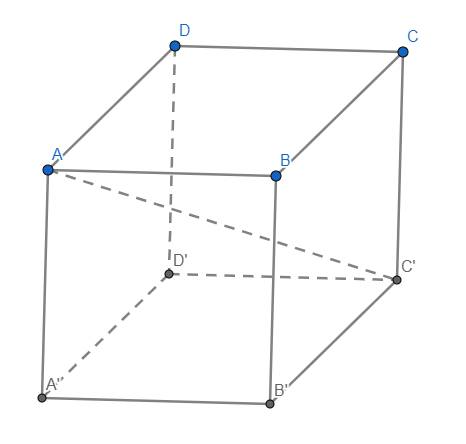
Ta có \(3AB^2=AC'^2=9a^2\) \(\Leftrightarrow AB^2=3a^2\Leftrightarrow AB=a\sqrt{3}\)
\(\Rightarrow V_{hlp}=AB^3=3a^3\sqrt{3}\) (đơn vị thể tích)
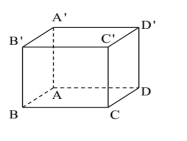 A.3a3 B.a3 C.a3
A.3a3 B.a3 C.a3
Lời giải:
Gọi độ dài cạnh của hình vuông $ABCD$ là $a$
Áp dụng định lý Pitago:
\(AB^2+AD^2=BD^2\Leftrightarrow a^2+a^2=8\)
\(\Rightarrow a=2\)
Do đó thể tích của hình hộp \(ABCD.A'B'C'D'\) là:
\(V=a^2h=a^2.AA'=2^2.8=32\) (cm khối)
Gọi đọ dài cạnh hình vuông ABCDlà a
Áp ụng định lý Pytago vào tam giác vuông ABD, ta có;
AB2+AD2=BD2\(\Leftrightarrow\)a2+a2=82=64
=>a\(\simeq5,7\)
Do đó thể tích hình hộp ABCD.A'B'C'D' là:
V=a2h=a2.AA'=5,72.12\(\simeq389,9\)(cm3)